Question

【题目】已知等差数列{an}中，a1=﹣2，公差d=3；数列{bn}中，Sn为其前n项和，满足：2nSn+1=2n（n∈N+）
（Ⅰ）记An= ，求数列An的前n项和S；
（Ⅱ）求证：数列{bn}是等比数列；
（Ⅲ）设数列{cn}满足cn=anbn ， Tn为数列{cn}的前n项积，若数列{xn}满足x1=c2﹣c1 ， 且xn= ，求数列{xn}的最大值．

Answer 1

【答案】（I）解：∵等差数列{an}中，a1=﹣2，公差d=3，
∴an=﹣2+3（n﹣1）=3n﹣5．
∴An= = = ，
∴数列An的前n项和S= + +…+
=
=﹣ ．
（II）证明：由2nSn+1=2n（n∈N+），可得 ．
当n=1时，a1=S1= ；
当n≥2时，bn=Sn﹣Sn﹣1= = ．
当n=1时也成立．
∴ = ．
∴数列{bn}是等比数列，首项为 ，公比为 ．
（III）数列{cn}满足cn=anbn= ．
数列{xn}满足x1=c2﹣c1= = ．
当n≥2时，xn= = =cn+1﹣cn= = ．
当n=1时也成立．
当n≤3时，数列{xn}单调递减；当n≥4时，数列{xn}单调递增，但是xn＜0．
∴数列{xn}的最大值是
【解析】（I）利用等差数列的通项公式可得an=3n﹣5．利用裂项可得An= ，利用“裂项求和”可得数列An的前n项和S．（II）由2nSn+1=2n（n∈N+），可得 ．当n=1时，b1=S1= ；当n≥2时，bn=Sn﹣Sn﹣1 ． 利用等比数列的通项公式即可证明．（III）数列{cn}满足cn=anbn= ．数列{xn}满足x1=c2﹣c1= ．当n≥2时，xn= =cn+1﹣cn= ．当n≤3时，数列{xn}单调递减；当n≥4时，数列{xn}单调递增，但是xn＜0，即可得出．
【考点精析】解答此题的关键在于理解等比关系的确定的相关知识，掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断，以及对数列的前n项和的理解，了解数列{an}的前n项和sn与通项an的关系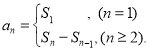．