题目内容
【题目】如图，点A，B是单位圆上的两点，A，B两点分别在第一、二象限，点C是圆与x轴正半轴的交点，角∠AOB= 
，若点A的坐标为（ 
， 
），记∠COA=α．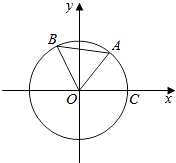 
（1）求 
的值；
（2）求点B的坐标．
【答案】
（1）解：∵A的坐标为（ 
， 
），根据三角函数的定义可知：sinα= ，cosα= ，
∴ 
= 
=32
（2）解：∵角∠AOB= 
，
∴cos∠COB=cos（α+ ）=cosαcos ﹣sinαsin =﹣ 
，
∴sin∠COB=sin（α+ ）=sinαcos +cosαsin = 
，
∴点B（﹣ ， ）
【解析】（1）由已知，根据三角函数的定义可求sinα，cosα的值，利用二倍角公式即可计算得解．（2）利用特殊角的三角函数值，两角和的正弦函数余弦函数公式分别求出cos∠COB，sin∠COB的值即可得解．
【考点精析】认真审题，首先需要了解同角三角函数基本关系的运用(同角三角函数的基本关系：
；
;（3） 倒数关系：
)．
练习册系列答案
相关题目
