题目内容
【题目】(本小题满分16分)已知数列![]() (
(![]() ,
, ![]() )满足
)满足![]() ,
,  其中
其中![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的取值范围;
的取值范围;
(2)设集合![]() .
.
①若![]() ,
, ![]() ,求证:
,求证: ![]() ;
;
②是否存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 都属于
都属于![]() ?若存在,请求出实数
?若存在,请求出实数![]() ,
, ![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() ,
, ![]() (2)①详见解析,②不存在
(2)①详见解析,②不存在
【解析】试题分析:(1)数列![]() 递推关系式是一个分段函数,可通过分段点进行连接:
递推关系式是一个分段函数,可通过分段点进行连接: ![]() ,
, ![]() ,
, ![]() ,根据对勾函数得
,根据对勾函数得![]() ,或
,或![]() ,从而有
,从而有![]() (2)①当
(2)①当![]() 时,数列
时,数列![]() 是一个等差数列,易得
是一个等差数列,易得![]() ,从而
,从而![]() ,令
,令![]() ,得
,得![]() .问题转化为证明
.问题转化为证明![]() 有满足条件
有满足条件![]() 解,易求得
解,易求得![]() ②
②![]() ∴
∴![]()
![]() ,问题转化为是否存在三个不同的整数
,问题转化为是否存在三个不同的整数![]() (
(![]() ),使得
),使得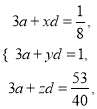 消去a,d得
消去a,d得![]() ,由于
,由于![]() ,所以无解
,所以无解
试题解析:(1)当![]() 时,
时,
![]() ,
, ![]() ,
, ![]() . 2分
. 2分
因为![]() ,
, ![]() ,或
,或![]() ,
,
所以![]() . 4分
. 4分
(2)①由题意![]() ,
, ![]() ,
, ![]() . 6分
. 6分
令![]() ,得
,得![]() .
.
因为![]() ,
, ![]() ,
,
所以令![]() ,则
,则![]() . 8分
. 8分
②不存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 同时属于
同时属于![]() . 9分
. 9分
假设存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 同时属于
同时属于![]() .
.
![]() ,∴
,∴![]() ,
,
从而![]() . 11分
. 11分
因为![]() ,
, ![]() ,
, ![]() 同时属于
同时属于![]() ,所以存在三个不同的整数
,所以存在三个不同的整数![]() (
(![]() ),
),
使得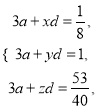 从而
从而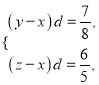
则![]() . 13分
. 13分
因为![]() 与
与![]() 互质,且
互质,且![]() 与
与![]() 为整数,
为整数,
所以![]() ,但
,但![]() ,矛盾.
,矛盾.
所以不存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 都属于
都属于![]() . 16分
. 16分

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目