题目内容
17.已知函数f(x)=2sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$的图象如图所示,则函数f(x)的解析式是( )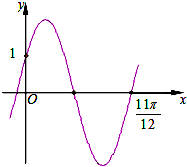
| A. | $f(x)=2sin({\frac{10}{11}x+\frac{π}{6}\;})$ | B. | $f(x)=2sin({\frac{10}{11}x-\frac{π}{6}\;})$ | ||
| C. | $f(x)=2sin({2x+\frac{π}{6}\;})$ | D. | $f(x)=2sin({2x-\frac{π}{6}\;})$ |
分析 由点(0,1)在函数图象上,可得1=2sinφ,结合|φ|<$\frac{π}{2}$,可得φ,又点($\frac{11π}{12}$,0)在函数图象上,可得0=2sin(ω$\frac{11π}{12}$+$\frac{π}{6}$),从而解得ω的一个值为2,从而得解.
解答 解:由函数图象可得:点(0,1)在函数图象上,故有:1=2sinφ,由于$,{|φ|<\frac{π}{2}}$,可得φ=$\frac{π}{6}$,
又点($\frac{11π}{12}$,0)在函数图象上,可得:0=2sin(ω$\frac{11π}{12}$+$\frac{π}{6}$),
由ω$\frac{11π}{12}$+$\frac{π}{6}$=2kπ,k∈Z,解得:ω=$\frac{24k-2}{11}$,k∈Z,ω>0,
当k=1时,可得:ω=2,
故选:C.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,确定ω的值是解题的关键,属于基本知识的考查.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
7.已知直线y=kx+2与圆 x2+y2=1没有公共点,则k的取值范围是( )
| A. | (-$\sqrt{2},\sqrt{2}}$) | B. | (-$\sqrt{3},\sqrt{3}}$) | C. | (-∞,-$\sqrt{2}}$)∪(${\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{3}}$)∪(${\sqrt{3}$,+∞) |
5.在一组样本数据(x1,y1),(x2,y2),…(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=2x+1上,则这组样本数据的样本相关系数为( )
| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
12.使cosx=1-m有意义的m的取值范围为( )
| A. | m≥0 | B. | 0≤m≤2 | C. | -1<m<1 | D. | m<-1或m>1 |
2.用秦九韶算法计算当x=2时,f(x)=3x4+x3+2x2+x+4的值的过程中,v2的值为( )
| A. | 3 | B. | 7 | C. | 16 | D. | 33 |
6.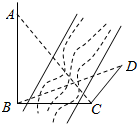 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)| A. | 10$\sqrt{2}$ | B. | 10$\sqrt{6}$ | C. | 10$\sqrt{3}$ | D. | 10 |
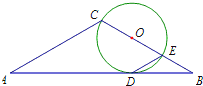 如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.
如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.