题目内容
6.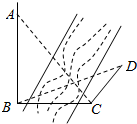 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)| A. | 10$\sqrt{2}$ | B. | 10$\sqrt{6}$ | C. | 10$\sqrt{3}$ | D. | 10 |
分析 设塔高为x米,根据题意可知在△ABC中,∠ABC=90°,∠ACB=60°,AB=x,从而有BC=$\frac{\sqrt{3}}{3}x$,在△BCD中,CD=10,∠BCD=105°,∠BDC=45°,∠CBD=30°,由正弦定理可求 BC,从而可求x即塔高.
解答 解:设塔高为x米,根据题意可知在△ABC中,∠ABC=90°,∠ACB=60°,AB=x,
从而有BC=$\frac{\sqrt{3}}{3}x$,AC=$\frac{2\sqrt{3}}{3}x$,
在△BCD中,CD=10,∠BCD=60°+30°+15°=105°,∠BDC=45°,∠CBD=30°
由正弦定理可得,$\frac{BC}{sin∠BDC}=\frac{CD}{sin∠CBD}$
可得,BC=$\frac{10sin45°}{sin30°}$=10$\sqrt{2}$=$\frac{\sqrt{3}}{3}x$
则x=10$\sqrt{6}$;
所以塔AB的高是10$\sqrt{6}$米;
故选:B.
点评 本题主要考查了正弦定理在实际问题中的应用,解决本题的关键是要把实际问题转化为数学问题,即正确建立数学模型,结合已知把题目中的数据转化为三角形中的数据,进而选择合适的公式进行求解.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
16.两直线x+y-1=0,x+y+1=0的距离是( )
| A. | 2 | B. | 1 | C. | 3 | D. | $\sqrt{2}$ |
17.已知函数f(x)=2sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$的图象如图所示,则函数f(x)的解析式是( )
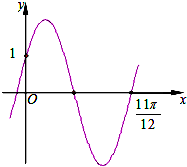

| A. | $f(x)=2sin({\frac{10}{11}x+\frac{π}{6}\;})$ | B. | $f(x)=2sin({\frac{10}{11}x-\frac{π}{6}\;})$ | ||
| C. | $f(x)=2sin({2x+\frac{π}{6}\;})$ | D. | $f(x)=2sin({2x-\frac{π}{6}\;})$ |
14.某中学为了解初三年级学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下:
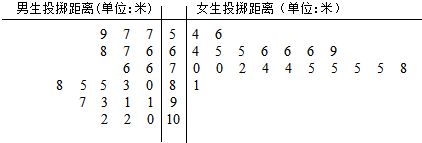
已知该项目评分标准为:
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,有6人的投掷距离低于7.0米,现从这6名男生中随机抽取2名男生,求抽取的2名男生得分都是4分的概率;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)

已知该项目评分标准为:
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
(Ⅱ)从上述20名男生中,有6人的投掷距离低于7.0米,现从这6名男生中随机抽取2名男生,求抽取的2名男生得分都是4分的概率;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)
1.某学校开设A类选修课3门,B类选修课4门,一位同学从中一共选3门,要求两类课必须选一门,则不同选法共( )
| A. | 30种 | B. | 35种 | C. | 42种 | D. | 48种 |
11.已知函数f(x)=x2-x+7,求f′(4)=( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |