题目内容
3.$\int_0^6{\sqrt{1-\frac{x^2}{36}}}$dx=$\frac{3π}{2}$.分析 根据定积分的几何意义,$\int_0^6{\sqrt{1-\frac{x^2}{36}}}$dx,表示以a=6,b=1焦点在x轴上的椭圆的面积的四分之一,再根据椭圆的面积公式S=πab,计算即可.
解答  解:$\int_0^6{\sqrt{1-\frac{x^2}{36}}}$dx,设1-$\frac{{x}^{2}}{36}$=y,y>0,$\frac{{x}^{2}}{36}$+y2=1,表示以a=6,b=1焦点在x轴上的椭圆的面积的四分之一,
解:$\int_0^6{\sqrt{1-\frac{x^2}{36}}}$dx,设1-$\frac{{x}^{2}}{36}$=y,y>0,$\frac{{x}^{2}}{36}$+y2=1,表示以a=6,b=1焦点在x轴上的椭圆的面积的四分之一,
如图所示,
∵S椭圆=πab=6π,
∴$\int_0^6{\sqrt{1-\frac{x^2}{36}}}$dx=$\frac{1}{4}$×6π=$\frac{3π}{2}$,
故答案为:$\frac{3π}{2}$.
点评 本题考查了定积分的几何意义,以及椭圆的面积公式,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
17.已知函数f(x)=2sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$的图象如图所示,则函数f(x)的解析式是( )
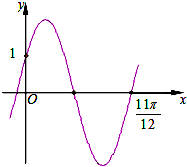

| A. | $f(x)=2sin({\frac{10}{11}x+\frac{π}{6}\;})$ | B. | $f(x)=2sin({\frac{10}{11}x-\frac{π}{6}\;})$ | ||
| C. | $f(x)=2sin({2x+\frac{π}{6}\;})$ | D. | $f(x)=2sin({2x-\frac{π}{6}\;})$ |
11.已知函数f(x)=x2-x+7,求f′(4)=( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
15.已知等差数列{an}和单调递减数列{bn}(n∈N*),{bn}通项公式为bn=λn2+a7•n.若a3,a11是方程x2-x-2=0的两根,则实数λ的取值范围是( )
| A. | (-∞,-3) | B. | $({-∞,-\frac{1}{6}})$ | C. | $({-\frac{1}{6},+∞})$ | D. | (-3,+∞) |