题目内容
7.已知直线y=kx+2与圆 x2+y2=1没有公共点,则k的取值范围是( )| A. | (-$\sqrt{2},\sqrt{2}}$) | B. | (-$\sqrt{3},\sqrt{3}}$) | C. | (-∞,-$\sqrt{2}}$)∪(${\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{3}}$)∪(${\sqrt{3}$,+∞) |
分析 当圆心到直线的距离大于半径时,直线与圆没有公共点,即可得出结论.
解答 解:直线y=kx+2可化为kx-y+2=0,
故圆心(0,0)到直线kx-y+2=0的距离d=$\frac{2}{\sqrt{{k}^{2}+1}}$>1,
解得k∈(-$\sqrt{3}$,$\sqrt{3}$),
故选:B.
点评 本题考查直线和圆的位置关系,考查点到直线的距离公式,属基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
2.若函数f(x)满足f(2)=3,且f(x+3)=3f(x),则f(2015)=( )
| A. | 3670 | B. | 3671 | C. | 3672 | D. | 3673 |
16.两直线x+y-1=0,x+y+1=0的距离是( )
| A. | 2 | B. | 1 | C. | 3 | D. | $\sqrt{2}$ |
17.已知函数f(x)=2sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$的图象如图所示,则函数f(x)的解析式是( )
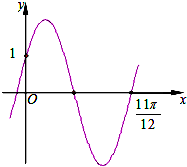

| A. | $f(x)=2sin({\frac{10}{11}x+\frac{π}{6}\;})$ | B. | $f(x)=2sin({\frac{10}{11}x-\frac{π}{6}\;})$ | ||
| C. | $f(x)=2sin({2x+\frac{π}{6}\;})$ | D. | $f(x)=2sin({2x-\frac{π}{6}\;})$ |
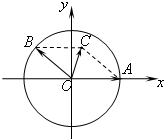 如图,在平面直角坐标系xOy上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在平面直角坐标系xOy上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).