题目内容
2.用秦九韶算法计算当x=2时,f(x)=3x4+x3+2x2+x+4的值的过程中,v2的值为( )| A. | 3 | B. | 7 | C. | 16 | D. | 33 |
分析 把所给的多项式写成关于x的一次函数的形式,依次写出,得到最后结果,从里到外进行运算,得到要求的值.
解答 解:f(x)=3x4+x3+2x2+x+4
=(((3x+1)x+2)x+1)x+4
∴在x=2时的值时,
V0=2
V1=3×2+1=7,
V1=7×2+2=16
故选:C.
点评 本题考查了秦九韶算法,属于基础题,本题解题的关键是对多项式进行整理,得到符合条件的形式.

练习册系列答案
相关题目
10.曲线y=x3-4x2+4在点(1,1)处的切线方程为( )
| A. | y=-x+2 | B. | y=5x-4 | C. | y=-5x+6 | D. | y=x-1 |
17.已知函数f(x)=2sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$的图象如图所示,则函数f(x)的解析式是( )
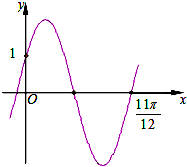

| A. | $f(x)=2sin({\frac{10}{11}x+\frac{π}{6}\;})$ | B. | $f(x)=2sin({\frac{10}{11}x-\frac{π}{6}\;})$ | ||
| C. | $f(x)=2sin({2x+\frac{π}{6}\;})$ | D. | $f(x)=2sin({2x-\frac{π}{6}\;})$ |
14.某中学为了解初三年级学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下:
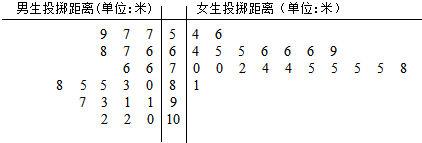
已知该项目评分标准为:
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,有6人的投掷距离低于7.0米,现从这6名男生中随机抽取2名男生,求抽取的2名男生得分都是4分的概率;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)

已知该项目评分标准为:
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
(Ⅱ)从上述20名男生中,有6人的投掷距离低于7.0米,现从这6名男生中随机抽取2名男生,求抽取的2名男生得分都是4分的概率;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)