题目内容

12．使cosx=1-m有意义的m的取值范围为（　　）
A．m≥0B．0≤m≤2C．-1＜m＜1D．m＜-1或m＞1

分析 根据余弦函数的有界性进行求解即可．

解答 解：∵-1≤cosx≤1，
∴由-1≤1-m≤1，
得0≤m≤2，
故选：B

点评 本题主要考查余弦函数的性质，利用余弦函数的有界性是解决本题的关键．

练习册系列答案
相关题目
2．若函数f（x）满足f（2）=3，且f（x+3）=3f（x），则f（2015）=（　　）
A．3670B．3671C．3672D．3673
3．已知P是△ABC内一点，$\overrightarrow{PB}$+$\overrightarrow{PC}$+2$\overrightarrow{PA}$=0，现将一粒黄豆随机投入△ABC内，则该粒黄豆落在△PAC内的概率是（　　）
A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{1}{5}$
20．在△ABC中，如果sinA=$\sqrt{3}$sinC，B=30°，那么角A=120°．
7．设双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两条渐近线交直线x=$\frac{{a}^{2}}{c}$于A，B两点，若以AB为直径的圆恰好过焦点F（c，0），则双曲线的离心率为$\sqrt{2}$．
17．已知函数f（x）=2sin（ωx+φ）$（{ω＞0，|φ|＜\frac{π}{2}}）$的图象如图所示，则函数f（x）的解析式是（　　）
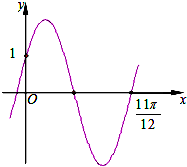
A．$f（x）=2sin（{\frac{10}{11}x+\frac{π}{6}\;}）$B．$f（x）=2sin（{\frac{10}{11}x-\frac{π}{6}\;}）$
C．$f（x）=2sin（{2x+\frac{π}{6}\;}）$D．$f（x）=2sin（{2x-\frac{π}{6}\;}）$
4．已知函数f（x）=lnx+ax2+（2-2a）x+$\frac{1}{4a}$（a＞0），若存在三个不相等的正实数x1，x2，x3，使得$\frac{{f（{x_1}）}}{x_1}=\frac{{f（{x_2}）}}{x_2}=\frac{{f（{x_3}）}}{x_3}$=3成立，则a的取值范围是（$\frac{1}{2e}$，$\frac{\sqrt{2}-1}{2}$）．
1．某学校开设A类选修课3门，B类选修课4门，一位同学从中一共选3门，要求两类课必须选一门，则不同选法共（　　）
A．30种B．35种C．42种D．48种
18．已知△ABC的顶点坐标分别为A（1，1），B（m，1），C（4，5），
（1）若m=5，求cos2A；
（2）若∠ABC为直角，求实数m的取值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网