题目内容
已知函数f(x)=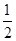 x2+lnx.
x2+lnx.
(1)求函数f(x)的单调区间;
(2)求证:当x>1时,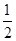 x2+lnx<
x2+lnx<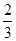 x3.
x3.
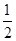 x2+lnx.
x2+lnx.(1)求函数f(x)的单调区间;
(2)求证:当x>1时,
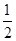 x2+lnx<
x2+lnx<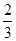 x3.
x3. (1) f(x)的单调增区间为(0,+∞) (2)略
本试题主要是考查了导数在研究函数中的运用。
(1)先求导,由导数研究函数的单调区间问题。
(2)构造新函数设g(x)=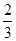 x3-
x3-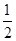 x2-lnx,
x2-lnx,
∴g′(x)=2x2-x-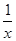 ,分析单调性得到证明。
,分析单调性得到证明。
(1)先求导,由导数研究函数的单调区间问题。
(2)构造新函数设g(x)=
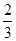 x3-
x3-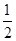 x2-lnx,
x2-lnx,∴g′(x)=2x2-x-
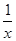 ,分析单调性得到证明。
,分析单调性得到证明。
练习册系列答案
相关题目
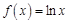 .
.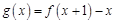 的最大值;
的最大值;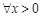 ,不等式
,不等式 恒成立,求实数
恒成立,求实数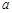 的取值范围;
的取值范围;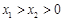 ,求证:
,求证: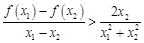 .
.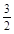 ,
,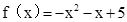
 ,
, .
. 的最大值;
的最大值;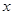 ,恒有
,恒有 成立,求实数
成立,求实数 的取值组成的集合.
的取值组成的集合.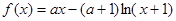 ..
..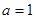 时,求
时,求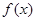 的单调区间;
的单调区间;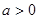 时,设
时,设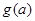 ,若
,若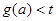 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围. ,
, ,
, .
. 在D内的极值点.
在D内的极值点. 若
若 在区间
在区间 上是减函数,则实数a的取值范围是 .
上是减函数,则实数a的取值范围是 . 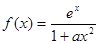 ,其中
,其中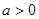
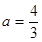 时,求
时,求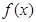 的极值点;
的极值点;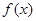 在定义域R内可导,若
在定义域R内可导,若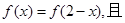
 ,若
,若 则
则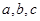 的大小关系是
的大小关系是


