题目内容
已知函数y=f(x)是定义在区间[-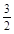 ,
,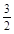 ]上的偶函数,且
]上的偶函数,且
x∈[0,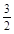 ]时,
]时,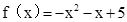
(1)求函数f(x)的解析式;
(2)若矩形ABCD的顶点A,B在函数y=f(x)的图像上,顶点C,D在x轴上,求矩形ABCD面积的最大值.
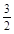 ,
,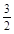 ]上的偶函数,且
]上的偶函数,且x∈[0,
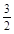 ]时,
]时,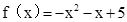
(1)求函数f(x)的解析式;
(2)若矩形ABCD的顶点A,B在函数y=f(x)的图像上,顶点C,D在x轴上,求矩形ABCD面积的最大值.
(1)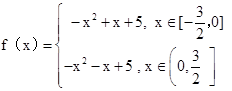 (2)6
(2)6
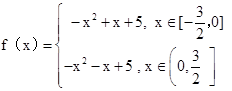 (2)6
(2)6本题主要考查了分段函数、函数的最值及其几何意义及利用导数研究函数的极值,属于中档题.
(1)欲求函数f(x)的解析式,只须求出函数f(x)在x∈[-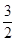 ,0]时的解析式即可,利用函数的偶函数性质即可由y轴右侧的表达式求出在y轴左侧的表达式.最后利用分段函数写出解析式即可.
,0]时的解析式即可,利用函数的偶函数性质即可由y轴右侧的表达式求出在y轴左侧的表达式.最后利用分段函数写出解析式即可.
(2)设A点在第一象限,坐标为A(t,-t2-t+5),利用对称性求出B点坐标,进而求出矩形ABCD面积,最后利用导数求出此面积表达式的最大值即可.
解(1)当x∈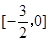 时,-x∈
时,-x∈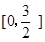 .
.
∴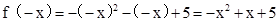 .又∵f(x)是偶函数,
.又∵f(x)是偶函数,
∴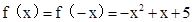 .
.
∴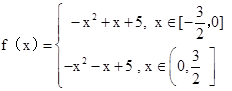 .
.
(2)由题意,不妨设A点在第一象限,
坐标为(t,-t2-t+5),其中t∈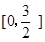
由图象对称性可知B点坐标为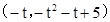 .
.
则S(t)= =
=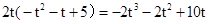
s′(t)=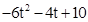 .由s′(t)=0,得
.由s′(t)=0,得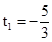 (舍去),
(舍去),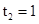 .
.
当0<t<1时,s′(t)>0;t>1时,s′(t)<0.
∴S(t)在(0,1]上单调递增,在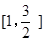 上单调递减.
上单调递减.
∴当t=1时,矩形ABCD的面积取得极大值6,
且此极大值也是S(t)在t∈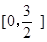 上的最大值.
上的最大值.
从而当t=1时,矩形ABCD的面积取得最大值6.
(1)欲求函数f(x)的解析式,只须求出函数f(x)在x∈[-
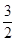 ,0]时的解析式即可,利用函数的偶函数性质即可由y轴右侧的表达式求出在y轴左侧的表达式.最后利用分段函数写出解析式即可.
,0]时的解析式即可,利用函数的偶函数性质即可由y轴右侧的表达式求出在y轴左侧的表达式.最后利用分段函数写出解析式即可.(2)设A点在第一象限,坐标为A(t,-t2-t+5),利用对称性求出B点坐标,进而求出矩形ABCD面积,最后利用导数求出此面积表达式的最大值即可.
解(1)当x∈
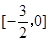 时,-x∈
时,-x∈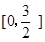 .
.∴
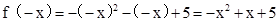 .又∵f(x)是偶函数,
.又∵f(x)是偶函数,∴
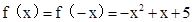 .
.∴
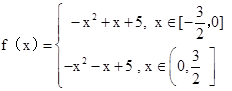 .
. (2)由题意,不妨设A点在第一象限,
坐标为(t,-t2-t+5),其中t∈
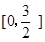
由图象对称性可知B点坐标为
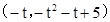 .
.则S(t)=
 =
=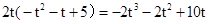
s′(t)=
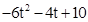 .由s′(t)=0,得
.由s′(t)=0,得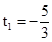 (舍去),
(舍去),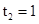 .
.当0<t<1时,s′(t)>0;t>1时,s′(t)<0.
∴S(t)在(0,1]上单调递增,在
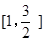 上单调递减.
上单调递减.∴当t=1时,矩形ABCD的面积取得极大值6,
且此极大值也是S(t)在t∈
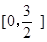 上的最大值.
上的最大值.从而当t=1时,矩形ABCD的面积取得最大值6.

练习册系列答案
相关题目
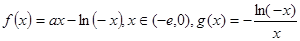 ,其中
,其中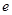 是自然常数,
是自然常数,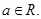
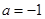 时,
时, 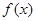 的单调性、极值;
的单调性、极值;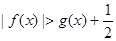 ;
;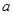 ,使
,使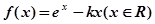
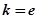 ,试确定函数
,试确定函数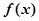 的单调区间;
的单调区间;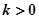 且对任意
且对任意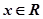 ,
,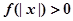 恒成立,试确定实数
恒成立,试确定实数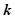 的取值范围;
的取值范围;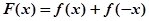 ,求证:
,求证: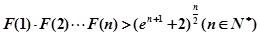
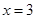 是函数
是函数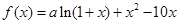 的一个极值点。
的一个极值点。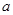 ;
;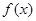 的单调区间;
的单调区间;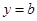 与函数
与函数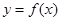 的图象有3个交点,求
的图象有3个交点,求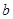 的取值范围。
的取值范围。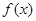 是定义在R上的奇函数,且
是定义在R上的奇函数,且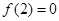 ,当x>0时,有
,当x>0时,有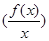 的导数小于零恒成立,则不等式
的导数小于零恒成立,则不等式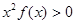 的解集是( )
的解集是( ) (2,+
(2,+  )
)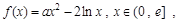 其中
其中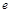 是自然对数的底 .
是自然对数的底 .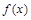 在
在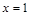 处取得极值,求
处取得极值,求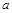 的值;
的值;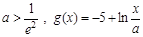 ,存在
,存在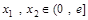 ,使得
,使得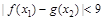 成立,求
成立,求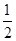 x2+lnx.
x2+lnx.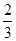 x3.
x3.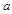 为实数,
为实数,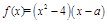 ,
,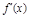 为
为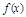 的导函数.
的导函数.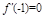 ,求
,求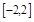 上的最大值和最小值;
上的最大值和最小值;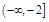 和
和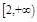 上均单调递增,求
上均单调递增,求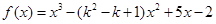 ,
,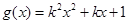 ,其中
,其中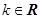 .
. 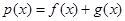 ,若
,若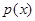 在区间
在区间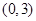 是单调函数,求
是单调函数,求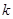 的取值范围;
的取值范围; ,是否存在
,是否存在 ,存在惟一的非零实数
,存在惟一的非零实数 (
( ),使得
),使得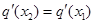 成立?若存在,求
成立?若存在,求