题目内容
设a<1,集合 ,
, ,
, .
.
(1)求集合D(用区间表示);
(2)求函数 在D内的极值点.
在D内的极值点.
 ,
, ,
, .
.(1)求集合D(用区间表示);
(2)求函数
 在D内的极值点.
在D内的极值点.(1)i)当0<a<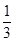 时,D=A∩B=(0,x1)∪(x2,+∞);
时,D=A∩B=(0,x1)∪(x2,+∞);
ii)当a≤0时,D=(x2,+∞).
(2)f(x)在D内单调递增.因此f(x)在D内没有极值点.
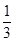 时,D=A∩B=(0,x1)∪(x2,+∞);
时,D=A∩B=(0,x1)∪(x2,+∞);ii)当a≤0时,D=(x2,+∞).
(2)f(x)在D内单调递增.因此f(x)在D内没有极值点.
(1)解本小题的关键是令h(x)=2x2-3(1+a)x+6a,根据Δ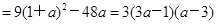 ,然后根据a的值分类讨论,求出h(x)>0的解集,从而可确定D.
,然后根据a的值分类讨论,求出h(x)>0的解集,从而可确定D.
(2)先求出f′(x)=6x2-6(1+a)x+6a=6(x-1)(x-a),然后再根据(1)中a在不同取值下对应的D,确定f(x)的极值.
解:(1)x∈D?x>0且2x2-3(1+a)x+6a>0.
令h(x)=2x2-3(1+a)x+6a,Δ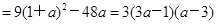 .
.
①当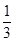 <a<1时,Δ<0,所以?x∈R,h(x)>0,所以B=R.于是D=A∩B=A=(0,+∞).
<a<1时,Δ<0,所以?x∈R,h(x)>0,所以B=R.于是D=A∩B=A=(0,+∞).
②当a=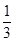 时,Δ=0,此时方程h(x)=0有唯一解,x1=x2=
时,Δ=0,此时方程h(x)=0有唯一解,x1=x2=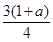 =
=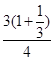 =1,
=1,
所以B=(-∞,1)∪(1,+∞).于是D=A∩B=(0,1)∪(1,+∞).
③当a<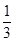 时,Δ>0,此时方程h(x)=0有两个不同的解x1=
时,Δ>0,此时方程h(x)=0有两个不同的解x1=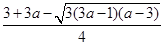 ,x2=
,x2=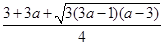 .
.
因为x1<x2且x2>0,所以B=(-∞,x1)∪(x2,+∞).
又因为x1>0?a>0,所以
i)当0<a<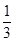 时,D=A∩B=(0,x1)∪(x2,+∞);
时,D=A∩B=(0,x1)∪(x2,+∞);
ii)当a≤0时,D=(x2,+∞).
(2)f′(x)=6x2-6(1+a)x+6a=6(x-1)(x-a).
当a<1时,f(x)在R上的单调性如下表:

①当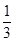 <a<1时,D=(0,+∞).由表可得,x=a为f(x)在D内的极大值点,x=1为f(x)在D内的极小值点.
<a<1时,D=(0,+∞).由表可得,x=a为f(x)在D内的极大值点,x=1为f(x)在D内的极小值点.
②当a=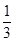 时,D=(0,1)∪(1,+∞).由表可得,x=
时,D=(0,1)∪(1,+∞).由表可得,x=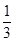 为f(x)在D内的极大值点.
为f(x)在D内的极大值点.
③当0<a<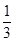 时,D=(0,x1)∪(x2,+∞).
时,D=(0,x1)∪(x2,+∞).
因为x1=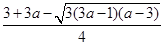 =
=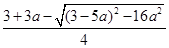 ≥
≥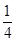 [3+3a-(3-5a)]=2a>a且x1<
[3+3a-(3-5a)]=2a>a且x1<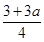 <1,
<1,
x2=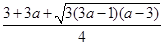 =
=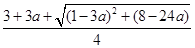 >
>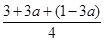 =1,
=1,
所以a∈D,1∉D.
由表可得,x=a为f(x)在D内的极大值点.
④当a≤0时,D=(x2,+∞)且x2>1.
由表可得,f(x)在D内单调递增.因此f(x)在D内没有极值点.
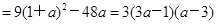 ,然后根据a的值分类讨论,求出h(x)>0的解集,从而可确定D.
,然后根据a的值分类讨论,求出h(x)>0的解集,从而可确定D.(2)先求出f′(x)=6x2-6(1+a)x+6a=6(x-1)(x-a),然后再根据(1)中a在不同取值下对应的D,确定f(x)的极值.
解:(1)x∈D?x>0且2x2-3(1+a)x+6a>0.
令h(x)=2x2-3(1+a)x+6a,Δ
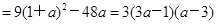 .
.①当
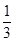 <a<1时,Δ<0,所以?x∈R,h(x)>0,所以B=R.于是D=A∩B=A=(0,+∞).
<a<1时,Δ<0,所以?x∈R,h(x)>0,所以B=R.于是D=A∩B=A=(0,+∞).②当a=
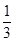 时,Δ=0,此时方程h(x)=0有唯一解,x1=x2=
时,Δ=0,此时方程h(x)=0有唯一解,x1=x2=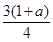 =
=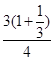 =1,
=1,所以B=(-∞,1)∪(1,+∞).于是D=A∩B=(0,1)∪(1,+∞).
③当a<
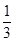 时,Δ>0,此时方程h(x)=0有两个不同的解x1=
时,Δ>0,此时方程h(x)=0有两个不同的解x1=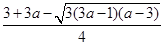 ,x2=
,x2=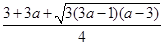 .
.因为x1<x2且x2>0,所以B=(-∞,x1)∪(x2,+∞).
又因为x1>0?a>0,所以
i)当0<a<
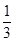 时,D=A∩B=(0,x1)∪(x2,+∞);
时,D=A∩B=(0,x1)∪(x2,+∞);ii)当a≤0时,D=(x2,+∞).
(2)f′(x)=6x2-6(1+a)x+6a=6(x-1)(x-a).
当a<1时,f(x)在R上的单调性如下表:

①当
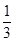 <a<1时,D=(0,+∞).由表可得,x=a为f(x)在D内的极大值点,x=1为f(x)在D内的极小值点.
<a<1时,D=(0,+∞).由表可得,x=a为f(x)在D内的极大值点,x=1为f(x)在D内的极小值点.②当a=
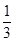 时,D=(0,1)∪(1,+∞).由表可得,x=
时,D=(0,1)∪(1,+∞).由表可得,x=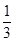 为f(x)在D内的极大值点.
为f(x)在D内的极大值点.③当0<a<
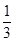 时,D=(0,x1)∪(x2,+∞).
时,D=(0,x1)∪(x2,+∞).因为x1=
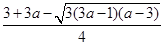 =
=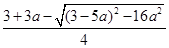 ≥
≥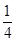 [3+3a-(3-5a)]=2a>a且x1<
[3+3a-(3-5a)]=2a>a且x1<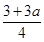 <1,
<1,x2=
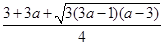 =
=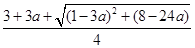 >
>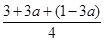 =1,
=1,所以a∈D,1∉D.
由表可得,x=a为f(x)在D内的极大值点.
④当a≤0时,D=(x2,+∞)且x2>1.
由表可得,f(x)在D内单调递增.因此f(x)在D内没有极值点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
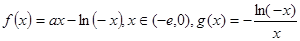 ,其中
,其中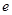 是自然常数,
是自然常数,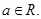
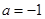 时,
时, 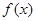 的单调性、极值;
的单调性、极值;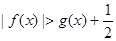 ;
;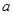 ,使
,使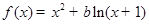 .
.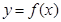 在定义域上是单调函数,求
在定义域上是单调函数,求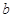 的取值范围;
的取值范围;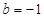 ,证明对于任意的
,证明对于任意的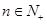 ,不等式
,不等式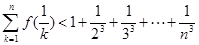 .
.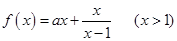
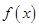 的最小值;
的最小值;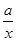 .
. 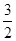 ,求a的值;
,求a的值;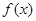 是定义在R上的奇函数,且
是定义在R上的奇函数,且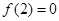 ,当x>0时,有
,当x>0时,有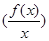 的导数小于零恒成立,则不等式
的导数小于零恒成立,则不等式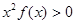 的解集是( )
的解集是( )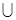 (2,+
(2,+ 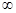 )
)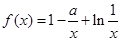 (
(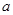 为实常数).
为实常数).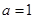 时,求函数
时,求函数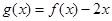 的单调区间;
的单调区间;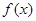 在区间
在区间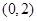 上无极值,求
上无极值,求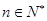 且
且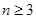 ,求证:
,求证: 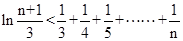 .
.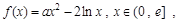 其中
其中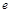 是自然对数的底 .
是自然对数的底 .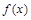 在
在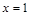 处取得极值,求
处取得极值,求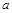 的值;
的值;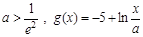 ,存在
,存在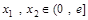 ,使得
,使得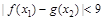 成立,求
成立,求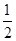 x2+lnx.
x2+lnx.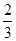 x3.
x3.