题目内容
14.已知数列{an},{bn},且a1=1,an+1+2an•an+1-an=0,2an+bn=1,(n∈N*).(1)计算a2,a3,a4,由此推测{an}的通项并给出证明;
(2)证明:(1-b1)(1-b2)+(1-b2)(1-b3)+…+(1-bn)(1-bn+1)<2.
分析 (1)分别根据a1=1,an+1+2an•an+1-an=0,即可求出a2,a3,a4的值,根据值可以猜想 ${a_n}=\frac{1}{2n-1},(n∈{N^*})$,并用数学归纳法证明.
(2)由(1)求出{1-bn}的通项,求出(1-bn)(1-bn+1)再根据裂项求和以及放缩法即可证明.
解答 解(1)当n=1时,a2+2a1•a2-a1=0,∴${a_2}=\frac{1}{3}$,
同理${a_3}=\frac{1}{5},{a_4}=\frac{1}{7}$,…(2分)
推测 ${a_n}=\frac{1}{2n-1},(n∈{N^*})$…(4分)
下面用数学归纳法证明:
①当n=2时,${a_2}=\frac{1}{3}=\frac{1}{2×1-1}$,∴等式成立.…(5分)
②假设n=k时等式成立,即${a_k}=\frac{1}{2k-1}$,…(6分)
那么,ak+1+2ak•ak+1-ak=0,
${a_{k+1}}(1+\frac{2}{2k-1})-\frac{1}{2k-1}=0$,
${a_{k+1}}=\frac{1}{2k+1}=\frac{1}{2(k+1)-1}$,
即当n=k+1时,${a_n}=\frac{1}{2n-1}$也成立,…(8分)
由①、②知对任意正整数n,${a_n}=\frac{1}{2n-1},(n∈{N^*})$都成立.…(9分)
(2)证明:∵2an+bn=1,∴$1-{b_n}=2{a_n}=\frac{2}{2n-1}$,…(10分)
∴$(1-{b_n})(1-{b_{n+1}})=\frac{2}{2n-1}×\frac{2}{2n+1}=2(\frac{1}{2n-1}-\frac{1}{2n+1})$,…(12分)
∴(1-b1)(1-b2)+(1-b2)(1-b3)+…+(1-bn)(1-bn+1),
=$2(\frac{1}{1}-\frac{1}{3})+2(\frac{1}{3}-\frac{1}{5})+…+2(\frac{1}{2n-1}-\frac{1}{2n+1})$,
=$2(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}-\frac{1}{2n+1})$,…(13分),
=$2(1-\frac{1}{2n+1})<2$…(14分)
点评 本题主要考查数列的通项公式的求法、前n项和公式的求法,考查抽象概括能力,推理论证能力,运算求解能力,考查化归与转化思想、裂项求和,属于中档题.

| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
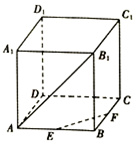 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | $ρ=4sin(θ+\frac{π}{3})$ | B. | $ρ=4sin(θ-\frac{π}{3})$ | C. | ρcosθ=2 | D. | ρsinθ=2 |
 在三棱锥PABC中,G为△ABC的重心,设$\overrightarrow{PA}$=a,$\overrightarrow{PB}$=b,$\overrightarrow{PC}$=c,则$\overrightarrow{PG}$=$\frac{1}{3}$($\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$)(用a,b,c表示).
在三棱锥PABC中,G为△ABC的重心,设$\overrightarrow{PA}$=a,$\overrightarrow{PB}$=b,$\overrightarrow{PC}$=c,则$\overrightarrow{PG}$=$\frac{1}{3}$($\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$)(用a,b,c表示).