题目内容

19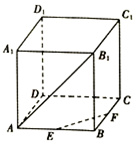．如图，在正方体ABCD-A1B1C1D1中，E、F分别为AB、BC中点，则异面直线EF与AB1所成角为（　　）
A．30°B．45°C．60°D．90°

分析 连接AC，B1C，可得∠CAB1为异面直线EF与AB1所成角，求出即可．

解答 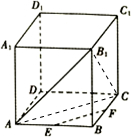解：连接AC，B1C，
∵△ABC中，E、F分别为AB、BC中点，
∴EF∥AC，
∴∠CAB1为异面直线EF与AB1所成角，
∵正方体ABCD-A1B1C1D1，
∴AC=AB1=B1C，即△AB1C为等边三角形，
∴∠CAB1=60°，
则异面直线EF与AB1所成角为60°，
故选：C．

点评 此题考查了异面直线及其所成的角，在立体几何中找平行线是解决问题的一个重要技巧，这个技巧就是通过三角形的中位线找平行线，如果试题的已知中涉及到多个中点，则找中点是出现平行线的关键技巧．

练习册系列答案
相关题目
9．已知a，b（a≠b）都是正有理数，$\sqrt{a}，\sqrt{b}$都是无理数．
（1）判断$\sqrt{a}•\sqrt{b}$是否可能是有理数，请举例说明；
（2）求证：$\sqrt{a}+\sqrt{b}$不可能是有理数．
10．计算：
（1）${（{2\frac{7}{9}}）^{0.5}}+{0.1^{-2}}+{（{2\frac{10}{27}}）^{-\frac{2}{3}}}-3{π^0}+\frac{37}{48}$；
（2）$\frac{{lg\sqrt{27}+lg8-3lg\sqrt{10}}}{lg1.2}$．
7．若向量$\overrightarrow a，\overrightarrow b$满足$|{\overrightarrow a}|=4，|{\overrightarrow b}|=6$，则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围是[2，10]．
14．已知数列{an}，{bn}，且a1=1，an+1+2an•an+1-an=0，2an+bn=1，（n∈N*）．
（1）计算a2，a3，a4，由此推测{an}的通项并给出证明；
（2）证明：（1-b1）（1-b2）+（1-b2）（1-b3）+…+（1-bn）（1-bn+1）＜2．
4．已知向量$\overrightarrow a=（1，2），\overrightarrow b=（1，0），\overrightarrow c=（3，4）$，若λ为实数，$（\overrightarrow a+λ\overrightarrow b）∥\overrightarrow c$，则λ=$\frac{1}{2}$．
11．若函数y=sin（ωx+$\frac{5π}{3}$）（ω＞0）的最小正周期是$\frac{π}{3}$，则ω=6．
8．sin164°sin224°+sin254°sin314°=$\frac{1}{2}$．（以具体数字作答）
10．函数f（x）=$\frac{1}{3}$x3-x2+1是减函数的区间为（　　）
A．（2，+∞）B．（-∞，2）C．（-∞，0）D．（0，2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网