题目内容
(本小题满分16分)函数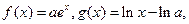 其中
其中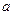 为常数,且函数
为常数,且函数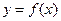 和
和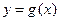 的图像在其与坐标轴的交点处的切线互相平行
的图像在其与坐标轴的交点处的切线互相平行
(1)、求函数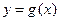 的解析式
的解析式
(2)、若关于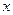 的不等式
的不等式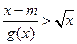 恒成立,求实数
恒成立,求实数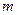 的取值范围。
的取值范围。
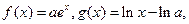 其中
其中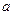 为常数,且函数
为常数,且函数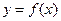 和
和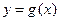 的图像在其与坐标轴的交点处的切线互相平行
的图像在其与坐标轴的交点处的切线互相平行(1)、求函数
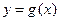 的解析式
的解析式(2)、若关于
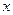 的不等式
的不等式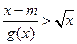 恒成立,求实数
恒成立,求实数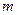 的取值范围。
的取值范围。(1)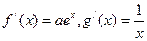 ------2
------2
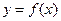 的图像与坐标轴的交点为
的图像与坐标轴的交点为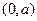 ,
,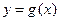 的图像与坐标轴的交点为
的图像与坐标轴的交点为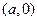
由题意得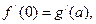 即
即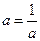 , ------3
, ------3
又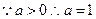
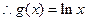 ------4
------4
(2)由题意
当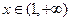 时,
时,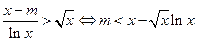 -------6
-------6
令
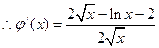 ------7
------7
令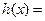
 ------9
------9
当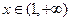 时,
时,
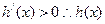 单调递增。
单调递增。
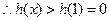 ------10
------10
由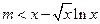 在
在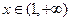 上恒成立,
上恒成立,
得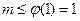 ------12
------12
当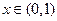 时,
时, ------13
------13
可得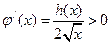
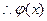 单调递增。------14
单调递增。------14
由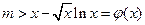 在
在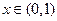 上恒成立,得
上恒成立,得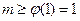 ------15
------15
综上,可知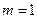 ------16
------16
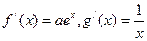 ------2
------2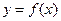 的图像与坐标轴的交点为
的图像与坐标轴的交点为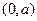 ,
,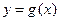 的图像与坐标轴的交点为
的图像与坐标轴的交点为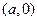
由题意得
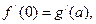 即
即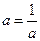 , ------3
, ------3又
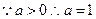
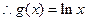 ------4
------4(2)由题意

当
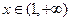 时,
时,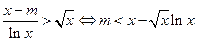 -------6
-------6令

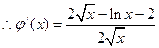 ------7
------7令
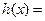
 ------9
------9当
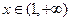 时,
时,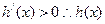 单调递增。
单调递增。 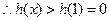 ------10
------10由
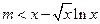 在
在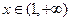 上恒成立,
上恒成立, 得
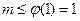 ------12
------12当
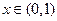 时,
时, ------13
------13可得
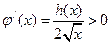
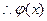 单调递增。------14
单调递增。------14由
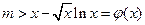 在
在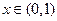 上恒成立,得
上恒成立,得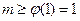 ------15
------15综上,可知
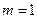 ------16
------16同答案

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为 . (Ⅰ)求函数
. (Ⅰ)求函数 的解析式;
的解析式;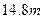 的钢条做一个长方体容器的框架.如果所做容器的低面的一边长比另以一边长多
的钢条做一个长方体容器的框架.如果所做容器的低面的一边长比另以一边长多 那么高是多少时容器的容积最大,并求出它的最大容积.
那么高是多少时容器的容积最大,并求出它的最大容积. 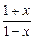 ,F(x)=
,F(x)=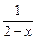 +f(x).
+f(x). 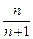 ;
;

 x3+x
x3+x 的另一点A,问电灯与点0的距离怎样,可使点A处有最大的照度?(
的另一点A,问电灯与点0的距离怎样,可使点A处有最大的照度?(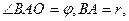 照度与
照度与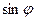 成正比,与
成正比,与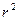 成反比)
成反比)
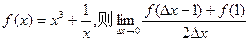 = .
= .