题目内容
设x1、x2为方程4x2-4mx+m+2=0的两个实根,当m=_________时,x12+x22有最小值_________.
: -1 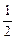
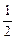
由韦达定理知: x1+x2=m,x1x2= ,
,
∴x12+x22=(x1+x2)2-2x1x2=m2- =(m-
=(m-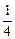 )2-
)2- ,
,
又x1,x2为实根,∴Δ≥0 ∴m≤-1或m≥2,
∴m≤-1或m≥2,
y=(m-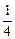 )2-
)2- 在区间(-∞,1)上是减函数,在[2,+∞
在区间(-∞,1)上是减函数,在[2,+∞ 上是增函数,又抛物线y开口向上且以m=
上是增函数,又抛物线y开口向上且以m=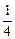 为对称轴. 故m=1时,ymin=
为对称轴. 故m=1时,ymin=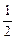 .
.
 ,
,∴x12+x22=(x1+x2)2-2x1x2=m2-
 =(m-
=(m-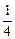 )2-
)2- ,
,又x1,x2为实根,∴Δ≥0
 ∴m≤-1或m≥2,
∴m≤-1或m≥2,y=(m-
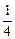 )2-
)2- 在区间(-∞,1)上是减函数,在[2,+∞
在区间(-∞,1)上是减函数,在[2,+∞ 上是增函数,又抛物线y开口向上且以m=
上是增函数,又抛物线y开口向上且以m=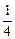 为对称轴. 故m=1时,ymin=
为对称轴. 故m=1时,ymin=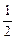 .
.
练习册系列答案
相关题目
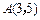 且与曲线
且与曲线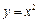 相切的直线方程.
相切的直线方程.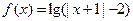 的定义域是( )
的定义域是( )
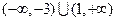
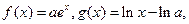 其中
其中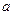 为常数,且函数
为常数,且函数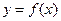 和
和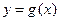 的图像在其与坐标轴的交点处的切线互相平行
的图像在其与坐标轴的交点处的切线互相平行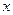 的不等式
的不等式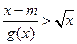 恒成立,求实数
恒成立,求实数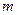 的取值范围。
的取值范围。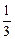 t3+2t2-5,则物体在t=3时的瞬时速度为______.
t3+2t2-5,则物体在t=3时的瞬时速度为______. =_________.
=_________.  ,则
,则 ( )
( )