题目内容
3.函数f(x)=x2+(2-6a)x+3a2(1)若函数对于任意的x总有f(2-x)=f(2+x)成立,求a的值.
(2)若函数在区间(5,6)上单调递增,求a的取值范围;
(3)当x∈[0,1]时,求函数的最小值.
分析 (1)根据图象的对称轴是x=2,解出a的值即可;(2)根据函数的单调性得到不等式,解出即可;(3)通过讨论对称轴的范围,从而求出函数的最小值.
解答 解:(1)若函数对于任意的x总有f(2-x)=f(2+x)成立,
则x=-$\frac{(2-6a)}{2}$=3a-1=2,解得:a=1;
(2)若函数在区间(5,6)上单调递增,
则对称轴x=3a-1≤5,解得:a≤2;
(3)对称轴x=3a-1<0时,即a<$\frac{1}{3}$时,f(x)min=f(0)=3a2,
对称轴x=3a-1在[0,1],即$\frac{1}{3}$≤a≤$\frac{2}{3}$时,f(x)min=f(3a-1)=6a-3,
对称轴x=3a-1>1,即a>$\frac{2}{3}$时,f(x)min=f(1)=3a2-6a+3.
点评 本题考察了函数的单调性,函数的最值问题,是一道中档题.

练习册系列答案
相关题目
18.设双曲线方程mx2-ny2=1(mn≠0),则“离心率e=$\sqrt{2}$”是“m=n”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.执行如图所示的程序框图,则输出结果S=( )
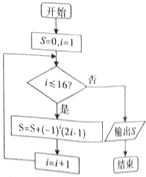

| A. | 14 | B. | 16 | C. | 19 | D. | 21 |
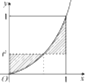 如图,由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是$\frac{1}{4}$.
如图,由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是$\frac{1}{4}$.