题目内容
13．
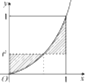如图，由曲线y=x2和直线y=t2（0＜t＜1），x=1，x=0所围成的图形（阴影部分）的面积的最小值是$\frac{1}{4}$．
分析 利用定积分表示出阴影部分的面积，计算定积分得到关于t的式子，求最小值．
解答 解：由曲线y=x2和直线y=t2（0＜t＜1），x=1，x=0所围成的图形（阴影部分）的面积为：S=${∫}_{0}^{t}（{t}^{2}-{x}^{2}）dx+{∫}_{t}^{1}（{x}^{2}-{t}^{2}）dx$=（t2x-$\frac{1}{3}{x}^{3}$）|${\;}_{0}^{t}$+（$\frac{1}{3}{x}^{3}$-t2x）|${\;}_{t}^{1}$=$\frac{2}{3}{t}^{3}+\frac{1}{3}-{t}^{2}+\frac{2}{3}{t}^{3}$=$\frac{4}{3}{t}^{3}-{t}^{2}+\frac{1}{3}$，
令S'=4t2-2t=0，解得t=$\frac{1}{2}$或t=0，而0＜t＜1，所以当t=$\frac{1}{2}$时，阴影部分的面积最小为$\frac{1}{4}$；
故答案为：$\frac{1}{4}$．
点评 本题考查了定积分的应用，关键是正确利用定积分表示阴影部分的面积．
练习册系列答案
相关题目
7．下列结论正确的是（ ）
| A． | 若a＞b，则ac＞bc | B． | 若a＞b，则a2＞b2 | ||
| C． | 若a+c＜b+c，c＜0，则a＞b | D． | 若$\sqrt{a}$＞$\sqrt{b}$，则a＞b |
18．箱子里有5个黄球，4个白球，每次随机取一个球，若取出黄球，则放回箱中重新取球，若取出白球，则停止取球，那么在4次取球之后停止取球的概率为（ ）
| A． | $\frac{3}{5}×\frac{1}{4}$ | B． | （$\frac{5}{9}$）3×$\frac{4}{9}$ | C． | 4×（$\frac{5}{9}$）3×$\frac{4}{9}$ | D． | 4×（$\frac{4}{9}$）3×$\frac{5}{9}$ |
2．某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：
（1）画出散点图；
（2）求回归直线方程；
（3）试预测广告支出为10百万元时，销售额多大？
（注：b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$，a=$\overline{y}-b\overline{x}$．
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
（2）求回归直线方程；
（3）试预测广告支出为10百万元时，销售额多大？
（注：b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$，a=$\overline{y}-b\overline{x}$．