题目内容
14. 如图所示,质量a=2.0kg的物体在水平外力的作用下在水平面上运动,已知物体运动过程中的坐标与时间的关系为 $\left\{\begin{array}{l}{x=3.0t(m)}\\{y=0.2{t}^{2}(m)}\end{array}\right.$,g=10m/s2 ,根据以上条件,求:
如图所示,质量a=2.0kg的物体在水平外力的作用下在水平面上运动,已知物体运动过程中的坐标与时间的关系为 $\left\{\begin{array}{l}{x=3.0t(m)}\\{y=0.2{t}^{2}(m)}\end{array}\right.$,g=10m/s2 ,根据以上条件,求:(1)t=10s时刻物体的位置坐标;
(2)t=10s时刻物体的速度和加速度的大小和方向.
分析 (1)根据物体运动过程中的关系式,求出在x、y轴方向上的对应值即可;
(2)根据题意,求出t=10时物体在x、y轴方向上的速度,求出速度与加速度的大小,再得出加速度的方向.
解答 解:(1)因为物体运动过程中的坐标与时间的关系为 $\left\{\begin{array}{l}{x=3.0t(m)}\\{y=0.2{t}^{2}(m)}\end{array}\right.$,
所以在x轴方向上,x=3.0t=3.0×10=30(m),
在y轴方向上,y=0.2t2=0.2×102=20(m),
所以,物体在t=10s时刻的位置坐标是(30m,20m);
(2)在x轴方向上,x=3.0t(m),
在y轴方向上,y=0.2t2(m),
又物体在这两个方向上的运动学公式为
x轴方向上,x=v0t,
在y轴方向上,y=$\frac{1}{2}$at2,
所以,$\left\{\begin{array}{l}{{v}_{0}t=3.0t}\\{\frac{1}{2}{at}^{2}=0.{2t}^{2}}\end{array}\right.$,
解得v0=3.0m/s,a=0.4m/s2;
所以,t=10s时,vy=0.4×10=4m/s,
v=$\sqrt{{{v}_{0}}^{2}{{+v}_{y}}^{2}}$=$\sqrt{{3}^{2}{+4}^{2}}$=5m/s;
所以,物体在t=10s时刻的速度为5m/s,
加速度的大小是0.4m/s2,
方向是y轴正方向.
点评 本题考查了运动的合成与分解的应用问题,也考查了函数关系的应用问题,是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.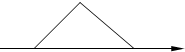 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
9. 如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
 如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )| A. | [$\frac{2}{3}$,2] | B. | [0,$\frac{2}{3}$] | C. | [1,2] | D. | [$\frac{2}{3}$,1] |
6.设集合A={(x,y)||x|+|y|≤1},若动点P(x,y)∈A,则x2+(y-1)2≤2的概率是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | π |
4.(x-2y)7的展开式中的第4项为( )
| A. | -35x4y3 | B. | 280x4y3 | C. | -280x4y3 | D. | 35x4y3 |
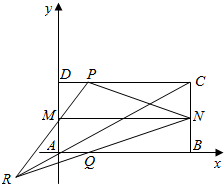 如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),
如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),