题目内容
5.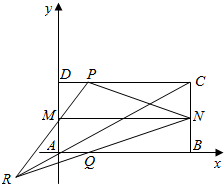 如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),
如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),(1)若$\overrightarrow{MP}⊥\overrightarrow{NP}$,求t的值
(2)求证:R,A,C三点共线.
分析 (1)求出相关向量,利用$\overrightarrow{MP}⊥\overrightarrow{NP}?\overrightarrow{MP}•\overrightarrow{NP}=0$,求解即可.
(2)R,M,P三点共线,设出$\overrightarrow{MR}=x\overrightarrow{MP}$,R,N,Q三点共线,可设$\overrightarrow{NR}=y\overrightarrow{NQ}$,然后列出方程组求解证明即可.
解答  解:(1)$\overrightarrow{MP}=(t,1)-(0,\frac{1}{2})=(t,\frac{1}{2}),\overrightarrow{NP}=(t,1)-(2,\frac{1}{2})=(t-2,\frac{1}{2})$…(3分
解:(1)$\overrightarrow{MP}=(t,1)-(0,\frac{1}{2})=(t,\frac{1}{2}),\overrightarrow{NP}=(t,1)-(2,\frac{1}{2})=(t-2,\frac{1}{2})$…(3分
)$\overrightarrow{MP}⊥\overrightarrow{NP}?\overrightarrow{MP}•\overrightarrow{NP}=0$,所以$t(t-2)+\frac{1}{4}=0$,$t=1±\frac{{\sqrt{3}}}{2}$…(6分)
(2)R,M,P三点共线,可设,$\overrightarrow{MR}=x\overrightarrow{MP}$
所以$\overrightarrow{AR}=\overrightarrow{AM}+x\overrightarrow{MP}=(xt,\frac{1}{2}(1+x))$R,N,Q三点共线,可设,$\overrightarrow{NR}=y\overrightarrow{NQ}$
所以$\overrightarrow{AR}=\overrightarrow{AN}+y\overrightarrow{NQ}=(2+y(t-2),\frac{1}{2}(1-y))$…(10分)
根据平面向量的基本定理得:$\left\{{\begin{array}{l}{xt=2+y(t-2)}\\{\frac{1}{2}(1+x)=\frac{1}{2}(1-y)}\end{array}}\right.$,解得:$x=\frac{1}{t-1},y=-\frac{1}{t-1}$
所以$\overrightarrow{AR}$=$(\frac{t}{t-1},\frac{t}{2(t-1)})=\frac{t}{2(t-1)}(2,1)=\frac{t}{2(t-1)}\overrightarrow{AC}$
所以R,A,C三点共线.…(15分)
点评 本题考查向量的应用,向量共线与垂直条件的应用,考查计算能力.

| A. | (1,-3),$\sqrt{2}$ | B. | (-1,3),2 | C. | (1,3),2 | D. | (-1,3),$\sqrt{2}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图所示,质量a=2.0kg的物体在水平外力的作用下在水平面上运动,已知物体运动过程中的坐标与时间的关系为 $\left\{\begin{array}{l}{x=3.0t(m)}\\{y=0.2{t}^{2}(m)}\end{array}\right.$,g=10m/s2 ,根据以上条件,求:
如图所示,质量a=2.0kg的物体在水平外力的作用下在水平面上运动,已知物体运动过程中的坐标与时间的关系为 $\left\{\begin{array}{l}{x=3.0t(m)}\\{y=0.2{t}^{2}(m)}\end{array}\right.$,g=10m/s2 ,根据以上条件,求: