题目内容
9.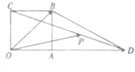 如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )| A. | [$\frac{2}{3}$,2] | B. | [0,$\frac{2}{3}$] | C. | [1,2] | D. | [$\frac{2}{3}$,1] |
分析 先建立以O为原点,以OD所在直线为x轴的直角坐标系,根据条件求出点P的坐标与α,β之间的关系;再根据点P的位置,借助于可行域即可求解.
解答  解:以O为原点,以OD所在直线为x轴建立直角坐标系,
解:以O为原点,以OD所在直线为x轴建立直角坐标系,
设点P(x,y),∵$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,
则(x,y)=α(1,1)+β(3,0)=(α+3β,α).
所以,$\left\{\begin{array}{l}x=α+3β\\ y=α\end{array}\right.$,∴α+β=$\frac{1}{3}$(x+2y).
由于点P为线段CD上的动点,目标函数为α+β=$\frac{1}{3}$(x+2y).
,如图所示,
当点P为点D(3,0)时,α+β=$\frac{1}{3}$(x+2y)取得最大值,其最大值为:1,
当点P为点C(0,1)时,α+β=$\frac{1}{3}$(x+2y)取得最小值,其最小值为:$\frac{2}{3}$,
故选:D.
点评 本题主要考查相等向量以及线性规划的简单应用问题,是对知识点的综合考查,属于综合性题目.

练习册系列答案
相关题目
19.双曲线$\frac{x^2}{4}-\frac{y^2}{2}$=1的渐近线方程是( )
| A. | y=±$\sqrt{2}$x | B. | y=±$\frac{{\sqrt{2}}}{2}$x | C. | y=±$\frac{1}{2}$x | D. | y=±2x |
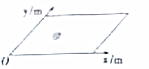 如图所示,质量a=2.0kg的物体在水平外力的作用下在水平面上运动,已知物体运动过程中的坐标与时间的关系为 $\left\{\begin{array}{l}{x=3.0t(m)}\\{y=0.2{t}^{2}(m)}\end{array}\right.$,g=10m/s2 ,根据以上条件,求:
如图所示,质量a=2.0kg的物体在水平外力的作用下在水平面上运动,已知物体运动过程中的坐标与时间的关系为 $\left\{\begin{array}{l}{x=3.0t(m)}\\{y=0.2{t}^{2}(m)}\end{array}\right.$,g=10m/s2 ,根据以上条件,求: