题目内容
6.设集合A={(x,y)||x|+|y|≤1},若动点P(x,y)∈A,则x2+(y-1)2≤2的概率是( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | π |
分析 本题是几何概型,集合A对应的区域是边长为$\sqrt{2}$的正方形,动点P(x,y)∈A,则x2+(y-1)2≤2的区域为以(0,1)为圆心,$\sqrt{2}$为半径的圆,利用面积比求概率.
解答 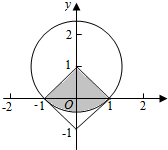 解:由题意,本题是几何概型,集合A对应的区域是边长为$\sqrt{2}$的正方形,面积为2,在此条件下,动点P(x,y)∈A,则x2+(y-1)2≤2的区域为以(0,1)为圆心,$\sqrt{2}$为半径的$\frac{1}{4}$圆,面积为$\frac{π}{2}$,如图
解:由题意,本题是几何概型,集合A对应的区域是边长为$\sqrt{2}$的正方形,面积为2,在此条件下,动点P(x,y)∈A,则x2+(y-1)2≤2的区域为以(0,1)为圆心,$\sqrt{2}$为半径的$\frac{1}{4}$圆,面积为$\frac{π}{2}$,如图
由几何概型公式得到x2+(y-1)2≤2的概率是$\frac{\frac{π}{2}}{2}=\frac{π}{4}$;
故选B.
点评 本题考查了几何概型概率的求法;根据明确集合A对应的区域以及x2+(y-1)2≤2对应的区域,利用几何概型公式解答.

练习册系列答案
相关题目
 如图所示,质量a=2.0kg的物体在水平外力的作用下在水平面上运动,已知物体运动过程中的坐标与时间的关系为 $\left\{\begin{array}{l}{x=3.0t(m)}\\{y=0.2{t}^{2}(m)}\end{array}\right.$,g=10m/s2 ,根据以上条件,求:
如图所示,质量a=2.0kg的物体在水平外力的作用下在水平面上运动,已知物体运动过程中的坐标与时间的关系为 $\left\{\begin{array}{l}{x=3.0t(m)}\\{y=0.2{t}^{2}(m)}\end{array}\right.$,g=10m/s2 ,根据以上条件,求: