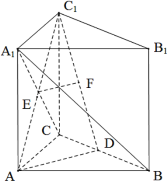
题目内容
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 和
和![]()
![]() ,过点
,过点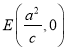 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,且
两点,且![]() ,
,![]() 。
。
(1)求椭圆的离心率;
(2)设点C与点A关于坐标原点对称,直线![]() 上有一点
上有一点![]() 在
在![]()
![]() 的外接圆上,求
的外接圆上,求![]() 的值
的值
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]() 且
且![]() ,得
,得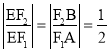 ,从而
,从而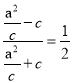 ,由此可以求出椭圆的离心率;(2)当
,由此可以求出椭圆的离心率;(2)当![]() 时,得
时,得![]() ,
, ![]() , 线段
, 线段![]() 的垂直平分线
的垂直平分线![]() 的方程为
的方程为![]() 直线
直线![]() 与
与![]() 轴的交点
轴的交点![]() 是
是![]() 外接圆的圆心,因此外接圆的方程为
外接圆的圆心,因此外接圆的方程为![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,由
,由 ,可以推导出
,可以推导出![]() 的值.
的值.
试题解析:(1)解:由![]() //
// ![]() 且
且![]() ,得
,得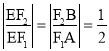 ,从而
,从而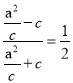
整理,得![]() ,故离心率
,故离心率![]()
(2)解法一:由(II)可知![]()
当![]() 时,得
时,得![]() ,由已知得
,由已知得![]() .
.
线段![]() 的垂直平分线l的方程为
的垂直平分线l的方程为![]() 直线l与x轴
直线l与x轴
的交点![]() 是
是![]() 外接圆的圆心,因此外接圆的方程为
外接圆的圆心,因此外接圆的方程为![]() .
.
直线![]() 的方程为
的方程为![]() ,于是点H(m,n)的坐标满足方程组
,于是点H(m,n)的坐标满足方程组
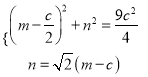 , 由
, 由![]() 解得
解得 故
故![]()
当![]() 时,同理可得
时,同理可得![]() .
.
解法二:由(II)可知![]()
当![]() 时,得
时,得![]() ,由已知得
,由已知得![]()
由椭圆的对称性可知B, ![]() ,C三点共线,因为点H(m,n)在
,C三点共线,因为点H(m,n)在![]() 的外接圆上,
的外接圆上,
且![]() ,所以四边形
,所以四边形![]() 为等腰梯形.
为等腰梯形.
由直线![]() 的方程为
的方程为![]() ,知点H的坐标为
,知点H的坐标为![]() .
.
因为![]() ,所以
,所以![]() ,解得m=c(舍),或
,解得m=c(舍),或![]() .
.
则![]() ,所以
,所以![]() .
.
当![]() 时同理可得
时同理可得![]() .
.
【 方法点睛】本题主要考查椭圆性质与离心率以及圆的方程与性质,属于难题.离心率的求解在圆锥曲线的考查中是一个重点也是难点,一般求离心率有以下几种情况:①直接求出![]() ,从而求出
,从而求出![]() ;②构造
;②构造![]() 的齐次式,求出
的齐次式,求出![]() ;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解.
;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解.

练习册系列答案
相关题目