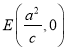题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2) 若函数![]() 有两个零点
有两个零点![]() ,
, ![]()
![]() ,且
,且![]() ,证明:
,证明: ![]() .
.
【答案】(1)当![]() 时,知
时,知![]() 在
在![]() 上递减;当
上递减;当![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;(2)证明见解析.
上递增;(2)证明见解析.
【解析】试题分析:
(1)由函数的解析式了的![]() ,
, ![]() ,分类讨论有:当
,分类讨论有:当![]() 时,知
时,知![]() 在
在![]() 上递减;当
上递减;当![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
(2)由(1)知, ![]() ,
, ![]() ,且
,且![]() ,故
,故![]() ,
, ![]() ,原问题等价于
,原问题等价于![]() ,结合单调性转化为
,结合单调性转化为![]() 即可,而
即可,而![]() ,
, ![]() ,构造函数,令
,构造函数,令![]() ,
, ![]() ,结合导函数的性质可得
,结合导函数的性质可得![]() ,即
,即![]() ,则结论得证.
,则结论得证.
试题解析:
(1)![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,知
,知![]() 在
在![]() 上是递减的;
上是递减的;
当![]() 时,
时, 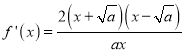 ,知
,知![]() 在
在![]() 上是递减的,在
上是递减的,在![]() 上递增的.
上递增的.
(2)由(1)知, ![]() ,
, ![]() ,
,
依题意![]() ,即
,即![]() ,
,
由![]() 得,
得, ![]() ,
, ![]() ,
, ![]() ,
,
由![]() 及
及![]() 得,
得, ![]() ,即
,即![]() ,
,
欲证![]() ,只要
,只要![]() ,
,
注意到![]() 在
在![]() 上是递减的,且
上是递减的,且![]() ,
,
只要证明![]() 即可,
即可,
由![]() 得
得![]() ,
,
所以![]()
![]()
![]()
![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,
,
则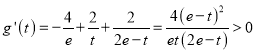 ,知
,知![]() 在
在![]() 上是递增的,于是
上是递增的,于是![]() ,即
,即![]() ,
,
综上, ![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】针对国家提出的延迟退休方案,某机构进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 | 保留 | 不支持 |
|
|
|
|
|
|
|
|
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“不支持”态度的人中抽取了
个人,已知从持“不支持”态度的人中抽取了![]() 人,求
人,求![]() 的值;
的值;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取![]() 人看成一个总体,从这
人看成一个总体,从这![]() 人中任意选取
人中任意选取![]() 人,求
人,求![]() 岁以下人数
岁以下人数![]() 的分布列和期望;
的分布列和期望;
(3)在接受调查的人中,有![]() 人给这项活动打出的分数如下:
人给这项活动打出的分数如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,把这
,把这![]() 个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过
个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过![]() 概率.
概率.
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y(万元)的几组对照数据:
x(年) | 2 | 3 | 4 | 5 | 6 |
y(万元) | 1 | 2.5 | 3 | 4 | 4.5 |
(1)若知道y对x呈线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?参考公式: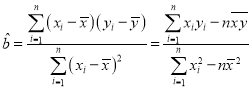 ,
,![]() .
.
【题目】2016年1月1日,我国全面实行二孩政策,某机构进行了街头调查,在所有参与调查的青年男女中,持“响应”“犹豫”和“不响应”态度的人数如下表所示:
响应 | 犹豫 | 不响应 | |
男性青年 | 500 | 300 | 200 |
女性青年 | 300 | 200 | 300 |
根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为犹豫与否与性别有关?请说明理由.
的把握认为犹豫与否与性别有关?请说明理由.
犹豫 | 不犹豫 | 总计 | |
男性青年 | |||
女性青年 | |||
总计 | 1800 |
参考公式:![]()
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |