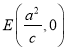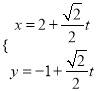题目内容
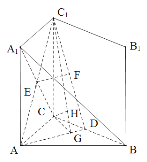
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]()
![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 中点.
中点.
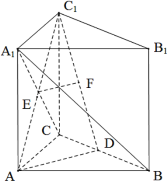
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用三角形的中位线性质可得![]() ,然后再利用线面平行的判定定理即可证出.
,然后再利用线面平行的判定定理即可证出.
(2)根据题意可证![]() ,
,![]()
![]() ,再利用线面垂直、面面垂直的判定定理即可证出.
,再利用线面垂直、面面垂直的判定定理即可证出.
(3)方法一:利用等体法![]() 即可求解;方法二:利用综合法,作
即可求解;方法二:利用综合法,作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,作
,作![]() ,垂足为
,垂足为![]() ,证出
,证出![]() 为点
为点![]() 到平面
到平面![]() 的距离,在直角
的距离,在直角![]() 中,求解即可.
中,求解即可.
(1)![]() 直三棱柱
直三棱柱![]() ,
,![]() 四边形
四边形![]() 为平行四边形
为平行四边形
![]() 为
为![]() 的中点
的中点 ![]()
![]() 为
为![]() 的中点,
的中点,![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
(2)![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]()
![]() 平行四边形
平行四边形![]() 为菱形,即
为菱形,即![]()
![]() 三棱柱
三棱柱![]() 为直三棱柱
为直三棱柱
![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面
平面![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
![]() 平面
平面![]()
(3)法一:(等体积法)连接![]() ,设点
,设点![]() 到平面
到平面![]() 的距离为
的距离为![]()
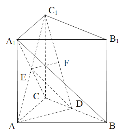
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() 为三棱锥
为三棱锥![]() 高,
高,
在直角![]() 中,
中,![]() ,
,![]() .
.
在直角![]() 中,
中,![]() ,
,![]() .
.
在直角![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
在等腰![]() 中,
中,![]() ,
,
![]() ,
,![]()
![]() ,
,
![]()
![]()
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]()
方法二:(综合法)作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,作
,作![]() ,垂足为
,垂足为![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() ,
,![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() , 即
, 即![]() 为点
为点![]() 到平面
到平面![]() 的距离,
的距离,
在直角![]() 中,
中,![]() ;在直角
;在直角![]() 中,
中,![]() ,
,
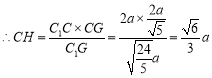
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】2016年1月1日,我国全面实行二孩政策,某机构进行了街头调查,在所有参与调查的青年男女中,持“响应”“犹豫”和“不响应”态度的人数如下表所示:
响应 | 犹豫 | 不响应 | |
男性青年 | 500 | 300 | 200 |
女性青年 | 300 | 200 | 300 |
根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为犹豫与否与性别有关?请说明理由.
的把握认为犹豫与否与性别有关?请说明理由.
犹豫 | 不犹豫 | 总计 | |
男性青年 | |||
女性青年 | |||
总计 | 1800 |
参考公式:![]()
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |