题目内容
【题目】(本小题满分13分)已知函数![]() (
(![]() 为常数,
为常数,![]() )
)
(1)若![]() 是函数
是函数![]() 的一个极值点,求
的一个极值点,求![]() 的值;
的值;
(2)求证:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(3)若对任意的![]() ,总存在
,总存在![]() ,使不等式
,使不等式![]() 成立,求正实数
成立,求正实数![]() 的取值范围.
的取值范围.
【答案】(1)2;(2)见解析;(3)![]() .
.
【解析】
试题分析:(1)利用函数在![]() 处的导数为0即可求出
处的导数为0即可求出![]() 的值;(2)利用函数的单调性与导数的关系跑到导函数在区间
的值;(2)利用函数的单调性与导数的关系跑到导函数在区间![]() 上恒大于0即可(3)若可导函数
上恒大于0即可(3)若可导函数![]() 在指定的区间
在指定的区间![]() 上单调递增(减),求参数问题,可转化为
上单调递增(减),求参数问题,可转化为![]()
![]() 恒成立,从而构建不等式,要注意“=”是否可以取到.
恒成立,从而构建不等式,要注意“=”是否可以取到.
试题解析: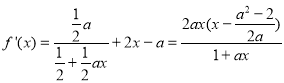 1分
1分
(1)由已知,得![]() 且
且![]() ,
,![]() 2分
2分
![]()
![]() 3分
3分
(2)当![]() 时,
时,![]()
![]() 4分
4分
![]() 当
当![]() 时,
时,![]() 又
又![]() 5分
5分
故![]() 在
在![]() 上是增函数
上是增函数
(3)![]() 时,由(2)知,
时,由(2)知,![]() 在
在![]() 上的最大值为
上的最大值为![]()
于是问题等价于:对任意的![]() ,不等式
,不等式![]() 恒成立. 7分
恒成立. 7分
记![]()
则![]() . 8分
. 8分
因为![]()
![]() 9分
9分
若![]() ,可知
,可知![]() 在区间
在区间![]() 上递减,在此区间上,有
上递减,在此区间上,有
![]() ,与
,与![]() 恒成立相矛盾,故
恒成立相矛盾,故![]() ,这时
,这时![]() , 12分
, 12分
![]() 在
在![]() 上递增,恒有
上递增,恒有![]() ,满足题设要求,
,满足题设要求,
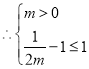 即
即![]()
![]() 实数
实数![]() 的取值范围为
的取值范围为![]() 14分
14分

练习册系列答案
相关题目