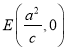题目内容
【题目】如图,在直三棱柱![]() 中,AB=BC,D、E分别为
中,AB=BC,D、E分别为![]() 的中点.
的中点.

(1)证明:ED为异面直线BB1与AC1的公垂线段;
(2)设AB=1, ![]() ,求二面角A1—AD—C1的大小.
,求二面角A1—AD—C1的大小.
【答案】(1)见解析;(2)60°.
【解析】试题分析:(1)设![]() 为
为![]() 中点,连接
中点,连接![]() ,先证明
,先证明![]() 是平行四边形,再证明
是平行四边形,再证明![]() 平面
平面![]() ,从而可得
,从而可得![]() 平面
平面![]() ,可得
,可得![]() 与直线
与直线![]() 与
与![]() 都垂直且相交,进而可得结论;(2)连接
都垂直且相交,进而可得结论;(2)连接![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,根据二面角的平面角定义可知
,根据二面角的平面角定义可知![]() 为二面角
为二面角![]() 的平面角,在直角三角形
的平面角,在直角三角形![]() 中求出正切值即可得结果.
中求出正切值即可得结果.
试题解析:(Ⅰ) 设O为AC中点,连接EO,BO,则EO![]()
![]() C1C,又C1C
C1C,又C1C![]() B1B,所以EO
B1B,所以EO![]() DB,EOBD为平行四边形,ED∥OB.
DB,EOBD为平行四边形,ED∥OB.
∵AB=BC,∴BO⊥AC,
又平面ABC⊥平面ACC1A1,BO面ABC,故BO⊥平面ACC1A1,
∴ED⊥平面ACC1A1,BD⊥AC1,ED⊥CC1,
∴ED⊥BB1,ED为异面直线AC1与BB1的公垂线.
解:(Ⅱ)连接A1E,由AB=1,AA1=AC=![]() 可知,A1ACC1为正方形,
可知,A1ACC1为正方形,
∴A1E⊥AC1,又由ED⊥平面ACC1A1和ED平面ADC1知平面
ADC1⊥平面A1ACC1,∴A1E⊥平面ADC1.作EF⊥AD,垂足为F,连接A1F,则A1F⊥AD,∠A1FE为二面角A1-AD-C1的平面角.
由已知AB=![]() ED=1, AA1=AC=
ED=1, AA1=AC=![]() ,∴
,∴![]() AE=A1E=1,
AE=A1E=1,
EF=![]() =
=![]() ,
,
tan∠A1FE=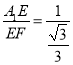 =
=![]() ,∴∠A1FE=60°.
,∴∠A1FE=60°.
所以二面角A1-AD-C1为60°.

【题目】针对国家提出的延迟退休方案,某机构进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 | 保留 | 不支持 |
|
|
|
|
|
|
|
|
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“不支持”态度的人中抽取了
个人,已知从持“不支持”态度的人中抽取了![]() 人,求
人,求![]() 的值;
的值;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取![]() 人看成一个总体,从这
人看成一个总体,从这![]() 人中任意选取
人中任意选取![]() 人,求
人,求![]() 岁以下人数
岁以下人数![]() 的分布列和期望;
的分布列和期望;
(3)在接受调查的人中,有![]() 人给这项活动打出的分数如下:
人给这项活动打出的分数如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,把这
,把这![]() 个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过
个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过![]() 概率.
概率.