题目内容
已知函数f(x)= +ln x(a≠0,a∈R).求函数f(x)的极值和单调区间.
+ln x(a≠0,a∈R).求函数f(x)的极值和单调区间.
 +ln x(a≠0,a∈R).求函数f(x)的极值和单调区间.
+ln x(a≠0,a∈R).求函数f(x)的极值和单调区间. 的极小值为1;单调递增区间为
的极小值为1;单调递增区间为 ,单调递减区间为
,单调递减区间为 。
。试题分析:先求导并整理变形,再令导数等于0,并求根。讨论导数的正负,导数大于0得增区间,导数小于0得减区间,根据单调性可得函数的极值。
因为
 ,
,令
 ,得
,得 ,
,又
 的定义域为
的定义域为 ,
, ,
, 随x的变化情况如下表:
随x的变化情况如下表:
所以
 时,
时, 的极小值为1.
的极小值为1. 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 .
.
练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 .
. 时,求函数
时,求函数 的极值;
的极值;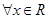 ,有
,有 成立,求实数
成立,求实数 的取值范围.
的取值范围. ,其中
,其中 ,则
,则 零点的个数是 ( )
零点的个数是 ( ) x2.
x2. 在
在 上的最小值是 .
上的最小值是 . 是减函数的区间为 ( )
是减函数的区间为 ( )



 在区间
在区间 上是单调递增函数,则实数
上是单调递增函数,则实数 的取值范围是 .
的取值范围是 .