题目内容
已知函数 .
.
(1)当 时,求函数
时,求函数 的极值;
的极值;
(2)若对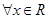 ,有
,有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 .
.(1)当
 时,求函数
时,求函数 的极值;
的极值;(2)若对
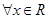 ,有
,有 成立,求实数
成立,求实数 的取值范围.
的取值范围.(1)极大值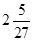 ,极小值
,极小值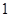 ;(2)
;(2)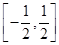 .
.
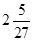 ,极小值
,极小值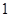 ;(2)
;(2)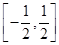 .
.试题分析:(1)将
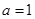 代入函数
代入函数 的解析式,利用导数结合表格求出函数
的解析式,利用导数结合表格求出函数 的极大值与极小值;(2)对
的极大值与极小值;(2)对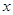 的符号进行分三类讨论①
的符号进行分三类讨论①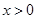 ;②
;②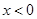 ;③
;③ ,主要是取绝对值符号,结合基本不等式求出参数
,主要是取绝对值符号,结合基本不等式求出参数 的取值范围,最后再相应地取
的取值范围,最后再相应地取 在三种情况下对应取值范围的交集.
在三种情况下对应取值范围的交集.(1)当
 时,
时,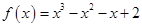 ,
,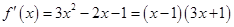 ,
,令
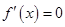 ,解得
,解得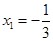 ,
,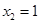 ,
,当
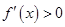 时,得
时,得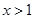 或
或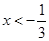 ;
;当
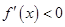 时,得
时,得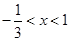 ,
,当
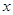 变化时,
变化时,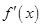 ,
, 的变化情况如下表:
的变化情况如下表: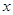 | 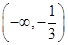 | 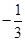 | 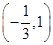 | 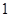 | 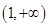 |
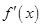 | 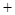 |  | 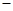 |  | 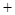 |
 | 单调递增 | 极大 | 单调递减 | 极小 | 单调递增 |
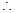 当
当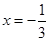 时,函数
时,函数 有极大值,
有极大值,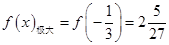 ,
, 当
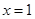 时函数
时函数 有极小值,
有极小值,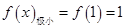 ;
;(2)
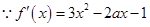 ,
,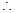 对
对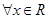 ,
, 成立,
成立,即
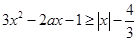 对
对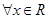 成立;
成立;①当
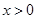 时,有
时,有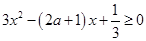 ,
,即
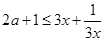 ,对
,对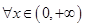 恒成立,
恒成立,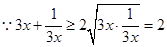 ,当且仅当
,当且仅当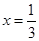 时等号成立,
时等号成立,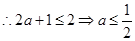 ;
; ②当
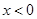 时,有
时,有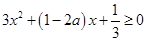 ,
,即
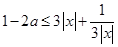 ,对
,对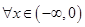 恒成立,
恒成立,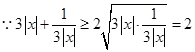 ,当且仅当
,当且仅当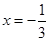 时等号成立,
时等号成立,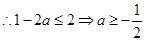 ,
, ③当
 时,
时,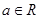
综上得实数
 的取值范围为
的取值范围为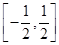 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, 的单调递减区间;
的单调递减区间; 上的最大值为20,求它在该区间上的最小值.
上的最大值为20,求它在该区间上的最小值. +ln x(a≠0,a∈R).求函数f(x)的极值和单调区间.
+ln x(a≠0,a∈R).求函数f(x)的极值和单调区间. ,若对于区间[-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是( )
,若对于区间[-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是( )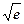 ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。 是可导的函数,且
是可导的函数,且 对于
对于 恒成立,则( )
恒成立,则( )