题目内容
5.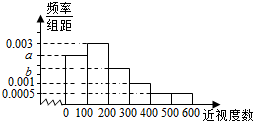 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:| 近视度数 | 0-100 | 100-200 | 200-300 | 300-400 | 400以上 |
| 学生频数 | 30 | 40 | 20 | 10 | 0 |
(Ⅰ)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(Ⅱ)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(Ⅲ)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.
分析 (Ⅰ)由频率分布表得到从该校任选1名高二学生,该生近视程度未达到中度及以上的频率得答案;
(Ⅱ)由频率分布直方图结合频率和为1求得从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(Ⅲ)分别求出EX、EY,由EX=EY求得b的值.
解答 解:(Ⅰ)由频数分布表可知,从该校任选1名高二学生,该生近视程度未达到中度及以上的频率为$\frac{70}{100}=0.7$,
则估计该生近视程度未达到中度及以上的概率为0.7;
(Ⅱ)若a=0.0024,则(0.003+0.0024+b+0.001+2×0.0005)×100=1,解得:b=0.0026.
则从该校任选1名高三学生,该生近视程度达到中度或中度以上的频率为(0.0026+0.001+2×0.0005)×100=0.46,
则从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率为0.46;
(Ⅲ)由频率分布表可得:P(X=0)=100a,P(X=1)=0.3,P(X=2)=100b+0.1,P(X=3)=0.1,
由频率分布直方图得:P(Y=0)=0.3,P(Y=1)=0.4,P(Y=2)=0.3,P(Y=3)=0,
则EX=1×0.3+200b+0.2+3×0.1=200b+0.8,
EY=1×0.4+2×0.3=1.
由EX=EY,得200b+0.8=1,解得:b=0.001.
点评 本题考查频率分布表,考查了频率分布直方图,考查了随机变量的分布列及其数学期望,是中档题.

练习册系列答案
相关题目
11.若曲线C1:x2+y2-2x=0与曲线C2:y(y-mx-m)=0有四个不同的交点,则实数m的取值范围是( )
| A. | (-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | B. | (-∞,-$\frac{\sqrt{3}}{3}$)∪($\frac{\sqrt{3}}{3}$,+∞) | C. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | D. | (-$\frac{\sqrt{3}}{3}$,0)∪(0,$\frac{\sqrt{3}}{3}$) |
 如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处,E,F分别为边AB,C1D的中点.
如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处,E,F分别为边AB,C1D的中点.