题目内容

19．已知等比数列{an}的首项a1=1，公比q=2，等差数列{bn}的首项b1=3，公差d=3，在{an}中插入{bn}中的项后从小到大构成新数列{cn}，则{cn}的第100项为（　　）
A．270B．273C．276D．279

分析 利用等差数列与等比数列的通项公式即可得出．

解答 解：由已知可得：an=2n-1，bn=3+3（n-1）=3n，
当n＜5时，an＜bn，当n≥5时，an＞bn，
∴在{an}中插入{bn}中的项后从小到大构成新数列{cn}，由3n＜16，3n＜32，3n＜64，3n＜128，3n＜256，3n＜512，…知，{cn}中插入{an}，{bn}中项的数目分别是4，5；1，5；1，11；1，11；1，43；1，85；即{cn}的第100项为等差数列{bn}中的第91项，
∴{cn}的第100项为273，
故选：B．

点评 本题考查了等差数列与等比数列的通项公式，考查了推理能力与计算能力，属于中档题

练习册系列答案
相关题目
5．已知圆C：x2+y2+6x-8y=0内有一点A（-5，0），直线l过点A交圆C于P，Q两点，若A为PQ中点，则|PQ|=2$\sqrt{5}$；若|PQ|=10，则l的方程为y=2x+10．
10．已知数列{an}的前n项和为Sn，且Sn+an=4，n∈N*
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）已知bn=2n-17（n∈N*），记cn=log2an-bn．求数列{cn}的前n项和Tn的最大值．
7．（1）将五本不同的书分给四个人有几种分法？
（2）将五本相同的书分给四个人有几种分法？
14．如图，设钝角α的顶点位于坐标原点O，始边与x轴的非负半轴重合，终边与单位圆O相交于点P，且点P的坐标为（-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$）．
（1）写出sinα和cosα的值；
（2）求sin（2α+$\frac{π}{6}$）的值．
4．已知数列{an}的前n项和为Sn，满足：Sn2+1=（an-2）Sn，n∈N*
（1）求S1，S2，S3，猜想Sn，并用数学归纳法证明；
（2）设${b_n}=（{2n+1}）{a_n}^2$，求证：对任意正整数n，有b1+b2+…+bn＜1．
11．已知f（x）=sin（$\frac{π}{4}$x+$\frac{π}{3}$）-$\sqrt{3}$cos（$\frac{π}{4}$x+$\frac{π}{4}$），则f（1）+f（2）+…+f（2008）+f（2009）=$\frac{\sqrt{2}}{2}$．
8．某程序框图如图所示，运行相应该程序，那么输出的k的值是（　　）
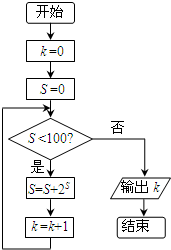
A．4B．5C．6D．7
9．已知sinα+cosα=$\frac{2}{3}$，则$\frac{1+tanα}{2si{n}^{2}α+sin2α}$=-$\frac{9}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网