题目内容

3．△ABC的内角A、B、C所对的边长分别为a，b，c，且C=2A，tanA=$\frac{\sqrt{7}}{3}$，a+c=5．
（1）求cosA及sinA的值．
（2）求b的长度．

分析 （1）根据同角三角函数基本关系求得sinA和cosA的值．
（2）根据正弦定理求得a和c的关系式，进而根据已知条件求得a和c，最后利用余弦定理求得b．

解答 解：（1）∵tanA=$\frac{\sqrt{7}}{3}$，
∴sinA=$\frac{\sqrt{7}}{4}$，cosA=$\frac{3}{4}$
（2）由正弦定理得$\frac{a}{c}$=$\frac{sinA}{sinC}$=$\frac{sinA}{sin2A}$=$\frac{sinA}{2sinAcosA}$=$\frac{1}{2}$$\frac{1}{cosA}$=$\frac{2}{3}$，
∴2c=3a，①
∵a+c=5．②
求得a=2，c=3
cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{{b}^{2}+9-4}{6b}$=$\frac{3}{4}$，
求得b=2或$\frac{5}{2}$．

点评 本题主要考查了正弦定理和余弦定理的运用．考查了学生对基础公式的灵活运用．

练习册系列答案
相关题目
9．求值：tan250°•sin80°•（$\sqrt{3}$tan20°-1）．
14．如图，设钝角α的顶点位于坐标原点O，始边与x轴的非负半轴重合，终边与单位圆O相交于点P，且点P的坐标为（-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$）．
（1）写出sinα和cosα的值；
（2）求sin（2α+$\frac{π}{6}$）的值．
11．已知f（x）=sin（$\frac{π}{4}$x+$\frac{π}{3}$）-$\sqrt{3}$cos（$\frac{π}{4}$x+$\frac{π}{4}$），则f（1）+f（2）+…+f（2008）+f（2009）=$\frac{\sqrt{2}}{2}$．
18．求函数y=tanx+|tanx|的图象，并求出其定义域、单调区间及最小正周期．
8．某程序框图如图所示，运行相应该程序，那么输出的k的值是（　　）
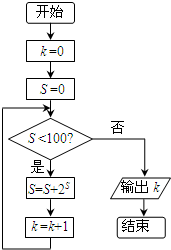
A．4B．5C．6D．7
15．甲、乙两袋中各装有大小相同的小球9个，其中甲袋中红色、黑色、白色小球的个数分别为2、3、4，乙袋中红色、黑色、白色小球的个数均为3，某人用左手从甲袋中取球，用右手从乙袋中取球，
（1）若左右手各取一球，求两只手中所取的球颜色不同的概率；
（2）若一次在同一袋中取出两球，如果两球颜色相同则称这次取球获得成功．某人第一次左手先取两球，第二次右手再取两球，记两次取球的获得成功的次数为随机变量X，求X的分布列和数学期望．
12．在等比数列{an}中，其前n项和为Sn，已知a3=$\frac{3}{2}$，S3=$\frac{9}{2}$．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）是否存在正整数n，使得Sn-Sn+2=$\frac{3}{32}$成立，若存在，求出n的值，若不存在，请说明理由．
13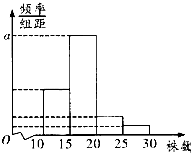．某单位组织职工开展构建绿色家园活动，在今年3月份参加义务植树活动的职工中，随机抽取M名职工为样本，得到这些职工植树的株数，根据此数据作出了频数与频率统计表和频率分布直方图如图：
（1）求出表中M，p及图中a的值；
（2）单位决定对参加植树的职工进行表彰，对植树株数在[25，30）区间的职工发放价值800元的奖品，对植树株数在[20，25）区间的职工发放价值600元的奖品，对植树株数在[15，20）区间的职工发放价值400元的奖品，对植树株数在[10，15）区间的职工发放价值200元的奖品，在所取样本中，任意取出2人，并设X为此二人所获得奖品价值之差的绝对值，求X的分布列与数学期望E（X）．
分组频数频率
[10，15）50.25
[15，20）12n
[20，25）mp
[25，30）10.05
合计M1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网