题目内容
2．某几何体的三视图如图，该几何体的体积为（ ）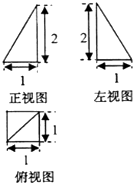
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | 1 | D． | 2 |
分析 通过观察几何体的三视图，可得该几何体是一个四棱锥，计算即得结论．
解答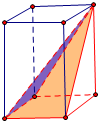 
解：根据几何体的三视图，得该几何体是一个四棱锥，
其底面为边长为1的正方形，高为2，
∴该四棱锥的体积为V四棱锥=$\frac{1}{3}$×1×1×2=$\frac{2}{3}$，
故选：B．
点评 本题主要考查几何体的体积，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
18．下列函数中，在其定义域内既是偶函数又在（-∞，0）上单调递增的函数是（ ）
| A． | f（x）=x2 | B． | f（x）=-log2|x| | C． | f（x）=3|x| | D． | f（x）=sinx |
19．已知抛物线y=ax2+bx+c（a≠0）的对称轴在y轴的左侧，其中a、b、c∈{-3，-2，-1，0，1，2，3}，在这些抛物线中，记随机变量X=|a-b|，则X的均值EX为（ ）
| A． | $\frac{8}{9}$ | B． | $\frac{3}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{3}$ |
如图，在四棱锥O-ABCD中，底面ABCD是边长为2的正方形，OA⊥底面ABCD，OA=2，M为OA的中点．则异面直线OB与MD所成角余弦值为$\frac{\sqrt{10}}{10}$．