题目内容

10．函数f（x）=$\frac{1}{3}$x3-3x2+5x+9的极大值点为x=1．

分析 求出f（x）的导函数，得出单调区间，即能求出极大值点．

解答 解：f′（x）=x2-6x+5；
f′（x）=0得，x=1，或5；
∴x∈（-∞，1）时，f′（x）＞0，
x∈（1，5）时，f′（x）＜0，
x∈（5，+∞）时，f′（x）＞0；
∴x=1是f（x）的极大值点．
故答案为：x=1．

点评 本题考查了，利用导数求函数的极值，考查了不等式的解法，属于基础题．

练习册系列答案
相关题目
6．已知单调递减的等比数列{an}满足a2+a3+a4=28，且a3+2是a2，a4是等差中项．
（1）求数列{an}的通项公式；
（2）若bn=log2an，求数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和Sn．
7．在△ABC中，角A、B、C的对边为a、b、c，则“A=B”成立的必要不充分条件为（　　）
A．cosA=cosBB．sinA=sinBC．bcosA=acosBD．acosA=bcosB
4．已知函数f（x）=cos（2x+$\frac{π}{3}$）+2sin2x．求f（x）在[-π，0]上的单调递减区间．
5．已知函数f（x）=$\frac{1}{3}$x3+$\frac{{{a^2}-1}}{2}$x2-a2x+a，x∈R，a∈R．
（1）若函数f（x）在区间[0，2]内恰有两个零点，求实数a的取值范围；
（2）若a=-1，设函数f（x）在区间[t，t+3]上的最大值为M（t），最小值为m（t），记F（t）=M（t）-m（t），求函数F（t）在区间[-3，-1]上的最小值．
15．设函数f（x）=$\frac{1}{x}$+ax+b，a，b∈R．
（1）若函数y=f（x）-2为奇函数，且函数f（x）在（0，1]上单调递减，在[1，+∞）上单调递增，求函数f（x）的解析式；
（2）当a=1时，方程f（x）=$\frac{1}{2}$x在区间（$\frac{1}{2}$，2]有两个不同的实数根，求实数b的最小值；
（3）若对任意的实数b，都存在实数x0∈[$\frac{1}{2}$，2]，使得不等式|f（x0）|≥$\frac{1}{2}$成立，求实数a的取值范围．
2．某几何体的三视图如图，该几何体的体积为（　　）
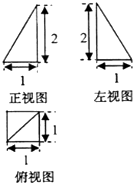
A．$\frac{1}{3}$B．$\frac{2}{3}$C．1D．2
19．已知两个函数f（x）=7x2-28x-c，g（x）=2x3+4x2-40x
（1）若对任意x∈[-3，3]，都有f（x）≤g（x）成立，求实数c的取值范围
（2）若对任意x1∈[-3，3]，x2∈[-3，3]，都有f（x1）≤g（x2）成立，求实数c的取值范围．
20．已知函数f（x）=lnx-$\frac{a（x-1）}{x+1}$，若函数f（x）在（0，+∞）上为增函数，则a的取值范围是（-∞，2]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网