题目内容
19.已知抛物线y=ax2+bx+c(a≠0)的对称轴在y轴的左侧,其中a、b、c∈{-3,-2,-1,0,1,2,3},在这些抛物线中,记随机变量X=|a-b|,则X的均值EX为( )| A. | $\frac{8}{9}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{3}$ |
分析 根据题意得出a•b>0,列出符合题意的事件即可,求解随机变量的概率,利用数学期望求解即.
解答 解:∵抛物线y=ax2+bx+c(a≠0)的对称轴在y轴的左侧,
∴$-\frac{b}{2a}$<0,
即a•b>0,
∵a、b、c∈{-3,-2,-1,0,1,2,3},
∴可得出:(a,b)的基本事件为:
(-3,-3)(-3,-2)(-3,-1)
(-2,-3)(-2,-2)(-2,-1)
(-1,-3)(-1,-2)(-1,-1)
(1,1)(1,2)(1.3)
(2,1)(2,2)(2.3)
(3,1)(3,2)(3.3)
共18个基本事件,
∵在这些抛物线中,记随机变量X=|a-b|,
∴可得出X=0,1,2,
P(X=0)=$\frac{6}{18}$=$\frac{1}{3}$
P(X=1)=$\frac{8}{18}$=$\frac{4}{9}$.
P(X=2)=$\frac{4}{18}$=$\frac{2}{9}$
∴分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{3}$ | $\frac{4}{9}$ | $\frac{2}{9}$ |
故选:A
点评 本题考查离散型随机变量的分布列的期望的求法,准确判断随机变量的取值,求出概率是解题的关键,判断a,b符合的条件.

练习册系列答案
相关题目
7.在△ABC中,角A、B、C的对边为a、b、c,则“A=B”成立的必要不充分条件为( )
| A. | cosA=cosB | B. | sinA=sinB | C. | bcosA=acosB | D. | acosA=bcosB |
2.某几何体的三视图如图,该几何体的体积为( )
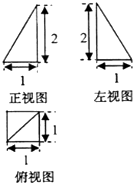

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
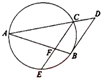 如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.