题目内容
17.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),过点(1,$\frac{1}{2}$)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆C的右焦点和上顶点(Ⅰ)求椭圆C的方程和离心率;
(Ⅱ)点P为椭圆C上任意一点,求△PAB面积的最大值.
分析 (Ⅰ)由题意可知:c=1,kOQ=$\frac{1}{2}$,则kAB=-2,由此能求出椭圆的标准方程.
(Ⅱ)设与直线AB的平行的直线方程为y=-2x+t,代入椭圆方程,由△=0得t=±2$\sqrt{6}$,故当t=-2$\sqrt{6}$时,求出点P到直线AB的最大距离,即可求△PAB面积的最大值.
解答 解:(Ⅰ)由题意,Q(1,$\frac{1}{2}$),可知:c=1,kOQ=$\frac{1}{2}$,则kAB=-2,…(3分)
所以直线AB的方程是y=-2(x-1),即y=-2x+2,即b=2.…(5分)
所以a2=b2+c2=5,
故椭圆的标准方程为$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1$.
椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}}{5}$------(7分)
(Ⅱ)设与直线AB的平行的直线方程为y=-2x+t,
代入椭圆方程得24x2-20tx+5t2-20=0,
由△=0得t=±2$\sqrt{6}$,
故当t=-2$\sqrt{6}$时,点P到直线AB的最大距离为d=$\frac{2(\sqrt{6}+1)}{\sqrt{5}}$,
又因为A(1,0),B($\frac{3}{5}$,$\frac{4}{5}$),所以|AB|=$\frac{2}{\sqrt{5}}$
故△PAB积的最大值$\frac{1}{2}|AB|d$=$\frac{1}{2}×$$\frac{2}{\sqrt{5}}$×$\frac{2(\sqrt{6}+1)}{\sqrt{5}}$=$\frac{2(\sqrt{6}+1)}{5}$------(14分)
点评 本题考查椭圆的方程与性质,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
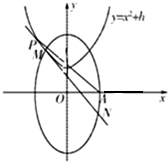 已知焦点在y轴上的椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)经过点Q($\frac{\sqrt{3}}{2}$,1),过椭圆的一个焦点且垂直长轴的弦长为1.
已知焦点在y轴上的椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)经过点Q($\frac{\sqrt{3}}{2}$,1),过椭圆的一个焦点且垂直长轴的弦长为1.