题目内容
14.在直角坐标系中,定义两点P(x1,y1)与Q(x2,y2)之间的“直角距离”为d(P,Q)=|x1-x2|+|y1-y2|,现给出四个命题:
(1)已知P(1,3),Q(sin2α,cos2α)(α∈R),则d(P,Q)为定值;
(2)已知P,Q,R三点不共线,则必有d(P,Q)+d(Q,R)>d(P,R);
(3)用|PQ|表示P,Q两点间的距离,那么|PQ|≥$\frac{{\sqrt{2}}}{2}$d(P,Q);
(4)若P,Q是椭圆$\frac{x^2}{9}+\frac{y^2}{4}$=1上的任意两点,则d(P,Q)的最大值是2$\sqrt{13}$.
在以上命题中,你认为正确的命题有①③④.(只填写所有正确的命题的序号)
分析 先根据直角距离的定义分别表示出所求的问题的表达式,然后根据集合中绝对值的性质进行判定即可.
解答 解:①已知P(1,3),Q(sin2α,cos2α)(α∈R),则d(P,Q)=|1-sin2α|+|3-cos2α|=cos2α+2+sin2α=3为定值,正确;
②设P(x,y),O(0,0),则d(0,P)=|x1-x2|+|y1-y2|=|x|+|y|=|x|+|x+1|,表示数轴上的x到1和0的距离之和,其最小值为1,故不正确;
③若|PQ|表示P、Q两点间的距离,那么|PQ|=$\sqrt{{(x}_{1}-{x}_{2})^{2}+{(y}_{1}-{y}_{2})^{2}}$,d(P,Q)=|x1-x2|+|y1-y2|,因为2(a2+b2)≥(a+b)2,所以|PQ|≥$\frac{\sqrt{2}}{2}$d(P,Q),正确;
④过P(1,3)与Q(5,7)的直线方程为y=x+2,点A到点P与Q的“直角距离”之和等于8,则|x-1|+|y-3|+|x-5|+|y-7|=2|x-1|+2|x-5|=8,所以|x-1|+|x-5|=4,所以1≤x≤5,
因为x∈Z,所以x=1,2,3,4,5,所以满足条件的点A只有5个,正确.
故答案为:①③④.
点评 本题考查两点之间的“直角距离”的定义,绝对值的意义,关键是明确P(x1,y1)、Q(x2,y2)两点之间的“直角距离”的含义.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
2.某几何体的三视图如图,该几何体的体积为( )
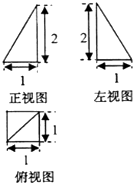

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |