题目内容
12.已知函数f(x)是R上的减函数,且y=f(x-2)的图象关于点(2,0)成中心对称.若不等式f(a+sinθ)+f(2+cos2θ)≥0 对任意θ∈R恒成立,则a的取值范围是(-∞,-$\frac{25}{8}$].分析 根据条件,确定函数的奇偶性,利用函数的奇偶性和单调性将不等式进行转化,利用三角函数的有界性求出函数的最值即可.
解答 解:∵函数y=f(x-2)的图象关于点(2,0)成中心对称,
∴函数y=f(x)的图象关于点(0,0)成中心对称,
即函数f(x)是奇函数,
则不等式f(a+sinθ)+f(2+cos2θ)≥0 等价为f(a+sinθ)≥-f(2+cos2θ)=f(-2-cos2θ),
∵定义在R上的函数y=f(x)是减函数,
∴a+sinθ≤-2-cos2θ,
即a≤-sinθ-2-cos2θ,
设g(θ)=-sinθ-2-cos2θ,
则g(θ)=-sinθ-2-(1-2sin2θ)=2sin2θ-sinθ-3=2(sinθ-$\frac{1}{4}$)2-$\frac{25}{8}$,
∵-1≤sinθ≤1
∴当sinθ=$\frac{1}{4}$时,g(θ)取得最小值-$\frac{25}{8}$,
∴要使a≤-sinθ-2-cos2θ恒成立,
∴a≤-$\frac{25}{8}$,
故实数a的取值范围是(-∞,-$\frac{25}{8}$],
故答案为:(-∞,-$\frac{25}{8}$]
点评 本题主要考查函数奇偶性和单调性的应用,利用函数恒成立转化为求函数的最值是解决本题的关键,综合性较强,有一定的难度.

练习册系列答案
相关题目
2.某几何体的三视图如图,该几何体的体积为( )
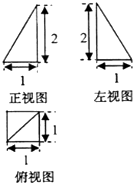

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
17.一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的体积为( )

| A. | 12+2$\sqrt{3}$+3π | B. | 12+3π | C. | $\sqrt{3}$π+2$\sqrt{3}$ | D. | $\frac{\sqrt{3}π}{3}$+2$\sqrt{3}$ |
2.复数z=1-i,则$\frac{1}{z}+{z^2}$对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 某校为宣传环境保护知识,随机抽取了部分学生进行“环境保护知识”测试,所有测试分数的分组区间为[50,70),[70,90),[90,110),[110,130),[130,150].如图是根据抽样测试所得的分数绘制的频率分布直方图.已知样本中分数小于90的人数是36,则样本中分数不小于70且小于130的人数是90.
某校为宣传环境保护知识,随机抽取了部分学生进行“环境保护知识”测试,所有测试分数的分组区间为[50,70),[70,90),[90,110),[110,130),[130,150].如图是根据抽样测试所得的分数绘制的频率分布直方图.已知样本中分数小于90的人数是36,则样本中分数不小于70且小于130的人数是90.