题目内容
11.已知函数f(x)=alnx+$\frac{1}{x}$(a≠0)(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若存在两条直线y=ax+b1,y=ax+b2(b1≠b2)都是曲线y=f(x)的切线.求实数a的取值范围;
(Ⅲ)若|x|f(x)≤0}⊆(0,1),求实数a的取值范围.
分析 (Ⅰ)先求出函数的导数,通过讨论a的符号,从而求出函数的单调区间;
(Ⅱ)问题转化为f′(x)=a至少有两个不等的正实根,根据二次函数的性质结合函数的单调性从而得到a的范围;
(Ⅲ)a<0时,不合题意,a>0时,通过讨论f($\frac{1}{a}$)的符号,结合函数的单调性,从而求出a的范围.
解答 解:(Ⅰ)f′(x)=$\frac{a}{x}$-$\frac{1}{{x}^{2}}$=$\frac{ax-1}{{x}^{2}}$(x>0),
当a<0时,f′(x)<0,则函数f(x)的单调递减区间是(0,+∞),
当a>0时,令f′(x)=0,得x=$\frac{1}{a}$,
当x变化时,f′(x),f(x)的变化情况如下:
| x | (0,$\frac{1}{a}$) | $\frac{1}{a}$ | ($\frac{1}{a}$,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↓ | 极小值 | ↑ |
(Ⅱ)若存在两条直线y=ax+b1,y=ax+b2(b1≠b2)都是曲线y=f(x)的切线,
∴f′(x)=a至少有两个不等的正实根,
令$\frac{ax-1}{{x}^{2}}$=a得ax2-ax+1=0,记其两个实根分别为x1,x2,
则$\left\{\begin{array}{l}{△{=a}^{2}-4a>0}\\{{x}_{1}{•x}_{2}=\frac{1}{a}>0}\end{array}\right.$,解得:a>4,
当a>4时,曲线y=f(x)在点(x1,f(x1)),(x2,f(x2))处的切线分别为:
y=ax+f(x1)-ax1,y=ax+f(x2)-ax2,
令F(x)=f(x)-ax(x>0),
由F′(x)=f′(x)-a=0得x=x1,x=x2(不防设x1<x2),
且当x1<x<x2时,F′(x)>0,即F(x)在[x1,x2]上是单调函数,
∴F(x1)≠F(x2);
∴y=ax+f(x1)-ax1,y=ax+f(x2)-ax2是曲线y=f(x)的两条不同的切线,
∴实数a的范围是(4,+∞);
(Ⅲ)当a<0时,函数f(x)是(0,+∞)内的减函数,
∵f(${e}^{-\frac{1}{a}}$)=aln(${e}^{-\frac{1}{a}}$)+$\frac{1}{{e}^{-\frac{1}{a}}}$=-1+$\frac{1}{{e}^{-\frac{1}{a}}}$=${e}^{\frac{1}{a}}$-1<0,而${e}^{-\frac{1}{a}}$∉(0,1),不符合题意,
当a>0时,由(Ⅰ)知:f(x)的最小值是f($\frac{1}{a}$)=-alna+a=a(1-lna),
①若f($\frac{1}{a}$)>0,即0<a<e时,{x|f(x)≤0}=∅⊆(0,1),
∴0<a<e符合题意,
②若f($\frac{1}{a}$)=0,即a=e时,{x|f(x)≤0}={$\frac{1}{e}$}⊆(0,1),
∴a=e符合题意,
③若f($\frac{1}{a}$)<0,即a>e时,有0<$\frac{1}{a}$<1,
∵f(1)=1>0,函数f(x)在($\frac{1}{a}$,+∞)内是增函数,
∴当x≥1时,f(x)>0,
又∵函数f(x)的定义域是(0,+∞),
∴{x|f(x)≤0}⊆(0,1),
∴a>e符合题意,
综上,实数a的范围是{a|a>0}.
点评 本题考察了函数的单调性的应用问题,考察导数的应用,考察分类讨论思想,第三问中通过讨论f($\frac{1}{a}$)的符号,再结合函数的单调性来求a的范围是解题的关键,本题是一道难题.

练习册系列答案
相关题目
7.在△ABC中,角A、B、C的对边为a、b、c,则“A=B”成立的必要不充分条件为( )
| A. | cosA=cosB | B. | sinA=sinB | C. | bcosA=acosB | D. | acosA=bcosB |
2.某几何体的三视图如图,该几何体的体积为( )
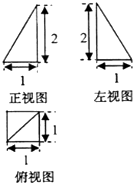

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
16.函数f(x)=(x-3)ex的单调递增区间是( )
| A. | (2,+∞) | B. | (0,3) | C. | (1,4) | D. | (-∞,2) |
 某校为宣传环境保护知识,随机抽取了部分学生进行“环境保护知识”测试,所有测试分数的分组区间为[50,70),[70,90),[90,110),[110,130),[130,150].如图是根据抽样测试所得的分数绘制的频率分布直方图.已知样本中分数小于90的人数是36,则样本中分数不小于70且小于130的人数是90.
某校为宣传环境保护知识,随机抽取了部分学生进行“环境保护知识”测试,所有测试分数的分组区间为[50,70),[70,90),[90,110),[110,130),[130,150].如图是根据抽样测试所得的分数绘制的频率分布直方图.已知样本中分数小于90的人数是36,则样本中分数不小于70且小于130的人数是90.