题目内容
已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)探究函数f(x)=ax+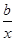 (a、b是正常数)在区间
(a、b是正常数)在区间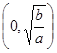 和
和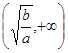 上的单调性(只需写出结论,不要求证明).并利用所得结论,求使方程f(x)-log4m=0有解的m的取值范围.
上的单调性(只需写出结论,不要求证明).并利用所得结论,求使方程f(x)-log4m=0有解的m的取值范围.
(1)求k的值;
(2)探究函数f(x)=ax+
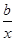 (a、b是正常数)在区间
(a、b是正常数)在区间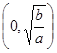 和
和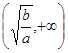 上的单调性(只需写出结论,不要求证明).并利用所得结论,求使方程f(x)-log4m=0有解的m的取值范围.
上的单调性(只需写出结论,不要求证明).并利用所得结论,求使方程f(x)-log4m=0有解的m的取值范围.(1)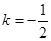 ;
;
(2)函数f(x)=ax+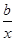 (a、b是正常数)在区间
(a、b是正常数)在区间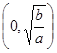 上为减函数,在区间
上为减函数,在区间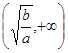 上为增函数;
上为增函数;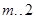 .
.
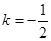 ;
;(2)函数f(x)=ax+
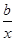 (a、b是正常数)在区间
(a、b是正常数)在区间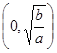 上为减函数,在区间
上为减函数,在区间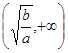 上为增函数;
上为增函数;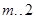 .
.试题分析:(1)由已知函数
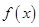 的定义域为
的定义域为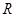 关于原点对称,又是偶函数,则可根据偶函数的定义
关于原点对称,又是偶函数,则可根据偶函数的定义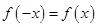 (或者利用特殊值代入计算亦可,如
(或者利用特殊值代入计算亦可,如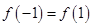 ),得到一个关于
),得到一个关于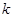 的方程,从而求出
的方程,从而求出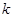 的值;(2)由函数
的值;(2)由函数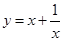 在区间
在区间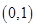 上为减函数,在区间
上为减函数,在区间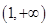 上为增函数,结合是可知函数
上为增函数,结合是可知函数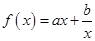 在区间
在区间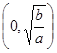 上为单调递减函数,在区间
上为单调递减函数,在区间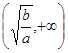 上为单调递增函数.由题意知方程
上为单调递增函数.由题意知方程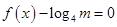 ,即为方程
,即为方程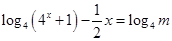 ,若使方程有解,则对数式
,若使方程有解,则对数式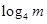 的值要在函数
的值要在函数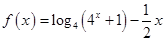 的值域范围内,所以首先要求出函数
的值域范围内,所以首先要求出函数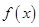 的值域,对函数
的值域,对函数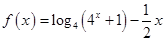 进行化归得
进行化归得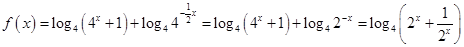 ,故原方程可化为
,故原方程可化为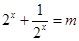 ,令
,令 ,
,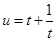 ,则
,则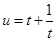 在区间
在区间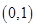 上为减函数,在区间
上为减函数,在区间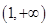 上为增函数,故函数
上为增函数,故函数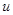 的最小值为
的最小值为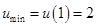 ,即当
,即当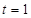 ,
,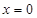 时函数
时函数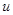 的值,所以函数
的值,所以函数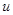 的值域为
的值域为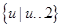 ,从而可求出
,从而可求出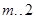 .
.试题解析:(1)由函数f(x)是偶函数,可知
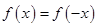 .
.∴
 .
. 即
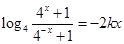 , 2分
, 2分 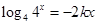 , 4分
, 4分∴
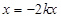 对一切
对一切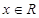 恒成立.∴
恒成立.∴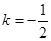 . 5分
. 5分(注:利用
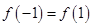 解出
解出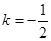 ,亦可得满分)
,亦可得满分)(2)结论:函数
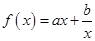 (a、b是正常数)在区间
(a、b是正常数)在区间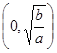 上为减函数,
上为减函数,在区间
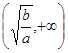 上为增函数. 6分
上为增函数. 6分由题意知,可先求
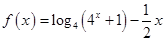 的值域,
的值域,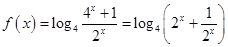 . 8分
. 8分设
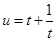 ,又设
,又设 ,则
,则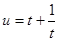 ,由定理,知
,由定理,知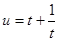 在
在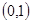 单调递减,在
单调递减,在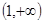 单调递增,所以
单调递增,所以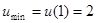 , 11分
, 11分∵
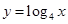 为增函数,由题意,只须
为增函数,由题意,只须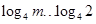 ,即
,即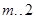
故要使方程
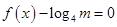 有解,
有解,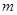 的取值范围为
的取值范围为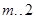 . 13分
. 13分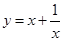 ;4.复合函数值域.
;4.复合函数值域.
练习册系列答案
相关题目
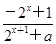 是奇函数,则a=________.
是奇函数,则a=________.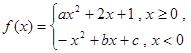 是偶函数,直线
是偶函数,直线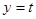 与函数
与函数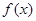 的图像自左至右依次交于四个不同点
的图像自左至右依次交于四个不同点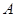 、
、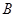 、
、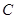 、
、 ,若
,若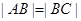 ,则实数
,则实数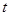 的值为________.
的值为________.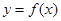 是
是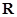 上的任意函数,下列叙述正确的是( )
上的任意函数,下列叙述正确的是( )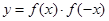 是奇函数
是奇函数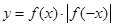 是奇函数
是奇函数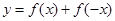 是偶函数
是偶函数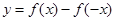 是偶函数
是偶函数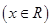 是偶函数,则下列各点中必在y=f(x)图象上的是( )
是偶函数,则下列各点中必在y=f(x)图象上的是( )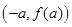
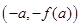
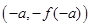
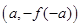
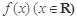 是偶函数,且
是偶函数,且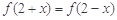 ,当
,当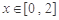 时,
时,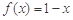 ,则方程
,则方程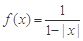 在区间
在区间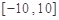 上的解的个数是( )
上的解的个数是( )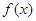 的图象形如字母M,奇函数
的图象形如字母M,奇函数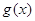 的图象形如字母N,若方程:
的图象形如字母N,若方程: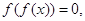
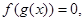
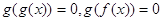 的实数根的个数分别为a、b、c、d,则
的实数根的个数分别为a、b、c、d,则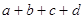 =( )
=( ) 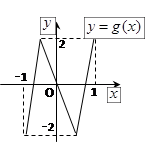
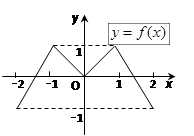
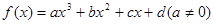 的对称中心为
的对称中心为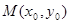 ,记函数
,记函数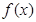 的导函数为
的导函数为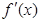 ,
,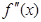 ,则有
,则有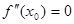 .若函数
.若函数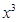 –
–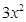 ,则可求得
,则可求得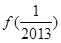 +
+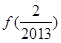 +
+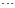
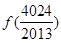 +
+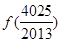 =( )
=( )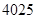
 为奇函数,且当
为奇函数,且当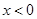 时,
时,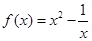 ,则
,则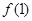 =( )
=( )