题目内容
9.已知实数a,b,c满足a>0,b>0,c>0,且abc=1.(Ⅰ)证明:(1+a)(1+b)(1+c)≥8;
(Ⅱ)证明:$\sqrt{a}+\sqrt{b}+\sqrt{c}≤\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$.
分析 (Ⅰ)利用$1+a≥2\sqrt{a},1+b≥2\sqrt{b},1+c≥2\sqrt{c}$,相乘即可证明结论.
(Ⅱ)利用$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=ab+bc+ac$,$ab+bc≥2\sqrt{a{b^2}c}=2\sqrt{b}$,$ab+ac≥2\sqrt{{a^2}{b^{\;}}c}=2\sqrt{a}$,$bc+ac≥2\sqrt{a{b^{\;}}{c^2}}=2\sqrt{c}$,相加证明即可.
解答 证明:(Ⅰ)$1+a≥2\sqrt{a},1+b≥2\sqrt{b},1+c≥2\sqrt{c}$,
相乘得:(1+a)(1+b)(1+c)≥8abc=8.
实数a,b,c满足a>0,b>0,c>0,且abc=1.(1+a)(1+b)(1+c)≥8------(5分)
(Ⅱ)$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=ab+bc+ac$,
$ab+bc≥2\sqrt{a{b^2}c}=2\sqrt{b}$,
$ab+ac≥2\sqrt{{a^2}{b^{\;}}c}=2\sqrt{a}$,
$bc+ac≥2\sqrt{a{b^{\;}}{c^2}}=2\sqrt{c}$,
相加得:$\sqrt{a}+\sqrt{b}+\sqrt{c}≤\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$------(10分)
点评 本题考查综合法证明不等式的方法的应用,考查逻辑推理能力.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
20.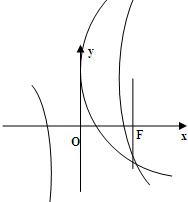 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )| A. | $\sqrt{2}$+1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$-1 |
17.原点与极点重合,x轴正半轴与极轴重合,则直角坐标为$(-2,-2\sqrt{3})$的点的极坐标是( )
| A. | $(4,\frac{π}{3})$ | B. | (4,$\frac{4π}{3}$) | C. | (-4,-$\frac{2π}{3}$) | D. | $(4,\frac{2π}{3})$ |
4.已知两个集合A={x|y=ln(-x2+x+2)},$B=\left\{{x\left|{\frac{2e+1}{e-x}≤2}\right.}\right\}$则A∩B=( )
| A. | $[{-\frac{1}{2},2})$ | B. | $({-1,-\frac{1}{2}}]$ | C. | (-1,e) | D. | (2,e) |
18.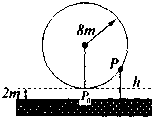 一个大风车的半径为8m,12min旋转一周,它的最低点P0离地面2m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
一个大风车的半径为8m,12min旋转一周,它的最低点P0离地面2m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
 一个大风车的半径为8m,12min旋转一周,它的最低点P0离地面2m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
一个大风车的半径为8m,12min旋转一周,它的最低点P0离地面2m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )| A. | h(t)=-8sin$\frac{π}{6}$t+10 | B. | h(t)=-cos$\frac{π}{6}$t+10 | C. | h(t)=-8sin$\frac{π}{6}$t+8 | D. | h(t)=-8cos$\frac{π}{6}$t+10 |