题目内容
14.函数f(x)=$\frac{x-1}{x+1}$(x∈R)的图象对称中心是(-1,1).分析 把原函数解析式变形得到y=f(x)=1-$\frac{2}{x+1}$,即y-1=$\frac{-2}{x+1}$,可设y′=y-1,x′=x+1,得到y′=$\frac{-2}{x′}$为反比例函数且为奇函数,求出对称中心即可得到所求中心.
解答 解:因为 y=f(x)=$\frac{x-1}{x+1}$=1-$\frac{2}{x+1}$,
即y-1=$\frac{-2}{x+1}$,
可设y′=y-1,x′=x+1,得到y′=$\frac{-2}{x′}$,
所以y′与x′成反比例函数关系且为奇函数,
则对称中心为(0,0)
即y′=0,x′=0得到y=1,x=-1
所以函数y=f(x)的对称中心为(-1,1 )
故答案为:(-1,1 ).
点评 本题考查学生灵活运用奇偶函数图象对称性的能力.考查类比猜测,合情推理的探究能力和创新精神.

练习册系列答案
相关题目
4.已知两个集合A={x|y=ln(-x2+x+2)},$B=\left\{{x\left|{\frac{2e+1}{e-x}≤2}\right.}\right\}$则A∩B=( )
| A. | $[{-\frac{1}{2},2})$ | B. | $({-1,-\frac{1}{2}}]$ | C. | (-1,e) | D. | (2,e) |
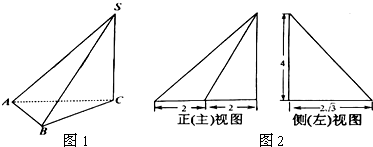
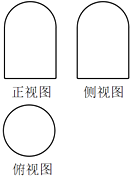 一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为7π.
一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为7π.