题目内容
19.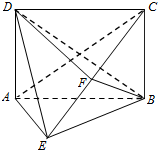 如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,
如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,(1)求证:AE∥平面BDF;
(2)求证:平面BDF⊥平面ACE;
(3)2AE=EB,在线段AE上找一点P,使得二面角P-DB-F的余弦值为$\frac{{\sqrt{10}}}{10}$,求AP的长.
分析 (1)根据线面平行的判定定理即可证明AE∥平面BDF;
(2)根据面面垂直的判定定理即可证明平面BDF⊥平面ACE;
(3)建立空间坐标系,求出平面的法向量,利用向量法即可得到结论.
解答 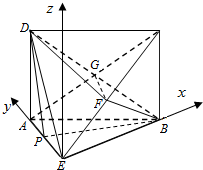 证明:(1)设AC∩BD=G,连接FG,易知G是AC的中点,
证明:(1)设AC∩BD=G,连接FG,易知G是AC的中点,
∵F是EC中点.
∴在△ACE中,FG∥AE,…(2分)
∵AE?平面BFD,FG?平面BFD,
∴AE∥平面BFD.…(4分)
(2)∵平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB,
∴BC⊥平面ABE,又∵AE?平面ABE,
∴BC⊥AE,
又∵AE⊥BE,BC∩BE=B,
∴AE⊥平面BCE,即AE⊥BF,…(6分)
在△BCE中,BE=CB,F为CE的中点,
∴BF⊥CE,AE∩CE=E,
∴BF⊥平面ACE,
又BF?平面BDF,
∴平面BDF⊥平面ACE.…(8分)
(3)如图建立坐标系,设AE=1,
则B(2,0,0),D(0,1,2),C(2,0,2),F(1,0,1),
设P(0,a,0),$\overrightarrow{BD}=(-2,1,2)$,$\overrightarrow{BF}=(-1,0,1)$,$\overrightarrow{PB}=(2,-a,0)$
设$\overrightarrow{n_1}$⊥面BDF,且$\overrightarrow{n_1}=({x_1},{y_1},{z_1})$,
则由$\overrightarrow{n_1}$⊥$\overrightarrow{BD}$得-2x1+y1+2z1=0,
由$\overrightarrow{n_1}$⊥$\overrightarrow{BF}$得-x1+z1=0,
令z1=1得x1=1,y1=0,从而$\overrightarrow{n_1}=(1,0,1)$…(10分)
设$\overrightarrow{n_2}$⊥面BDP,且$\overrightarrow{n_2}=({x_2},{y_2},{z_2})$,则
由$\overrightarrow{n_2}$⊥$\overrightarrow{BD}$得-2x2+y2+2z2=0,
由$\overrightarrow{n_2}$⊥$\overrightarrow{PB}$得2x2-ay2=0,
令y2=2得x2=a,z2=a-1,从而$\overrightarrow{n_2}=(a,2,a-1)$,
$cosθ=\frac{{|\overrightarrow{n_1}•\overrightarrow{n_2}|}}{{|\overrightarrow{n_1}|•|\overrightarrow{n_2}|}}=\frac{|a+a-1|}{{\sqrt{2}•\sqrt{{a^2}+4+{{(a-1)}^2}}}}=\frac{{\sqrt{10}}}{10}$,
解得a=0或a=1(舍)
即P在E处.…(14分)
点评 本题主要考查空间平行和垂直的位置关系的判断,以及二面角的应用,建立空间坐标系,利用向量法是解决本题的关键.

| A. | (1,2) | B. | [1,2] | C. | [-1,1) | D. | (-1,1) |
| A. | $[{-\frac{1}{2},2})$ | B. | $({-1,-\frac{1}{2}}]$ | C. | (-1,e) | D. | (2,e) |
| A. | f(2a)<f(3)<f(log2a) | B. | f(3)<f(log2a)<f(2a) | C. | f(log2a)<f(3)<f(2a) | D. | f(log2a)<f(2a)<f(3) |
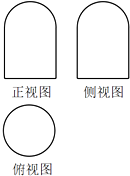 一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为7π.
一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为7π.