题目内容
14.某几何体三视图如图,根据图中标出的尺寸(单位:cm)可得该几何体的体积是6cm3(V柱体=Sh)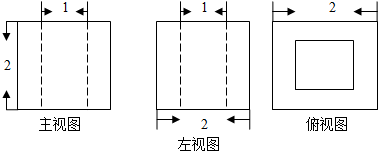
分析 由已知中的三视图,可知该几何体是一个以俯视图为底面的大长方体挖去一个小长方体所得组合体,分别计算底面面积和高,代入柱体体积公式,可得答案.
解答 解:由已知中的三视图,可知该几何体是一个以俯视图为底面的大长方体挖去一个小长方体所得组合体,
其底面面积S=2×2-1×1=3cm2,
高h=2cm,
故柱体的体积V柱体=Sh=6cm3,
故答案为:6cm3
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
6.已知tan(π-α)=-2,则$\frac{1}{{cos2α+{{cos}^2}α}}$=( )
| A. | -3 | B. | $\frac{2}{5}$ | C. | 3 | D. | $-\frac{5}{2}$ |
4.已知两个集合A={x|y=ln(-x2+x+2)},$B=\left\{{x\left|{\frac{2e+1}{e-x}≤2}\right.}\right\}$则A∩B=( )
| A. | $[{-\frac{1}{2},2})$ | B. | $({-1,-\frac{1}{2}}]$ | C. | (-1,e) | D. | (2,e) |
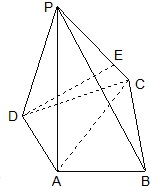 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1,点E在棱PC上,且DE⊥PB.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1,点E在棱PC上,且DE⊥PB.