题目内容
12.函数y=log3x-1$\frac{\sqrt{2x+3}}{x-1}$的定义域为(1,+∞).分析 根据函数成立的条件即可求函数的定义域.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{2x+3≥0}\\{x-1>0}\\{3x-1>0}\\{3x-1≠1}\end{array}\right.$,即$\left\{\begin{array}{l}{x≥-\frac{3}{2}}\\{x>1}\\{x>\frac{1}{3}}\\{x≠\frac{2}{3}}\end{array}\right.$,解得x>1,
即函数的定义域为(1,+∞),
故答案为:(1,+∞)
点评 本题主要考查函数定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
相关题目
20.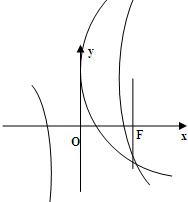 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )| A. | $\sqrt{2}$+1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$-1 |
17.原点与极点重合,x轴正半轴与极轴重合,则直角坐标为$(-2,-2\sqrt{3})$的点的极坐标是( )
| A. | $(4,\frac{π}{3})$ | B. | (4,$\frac{4π}{3}$) | C. | (-4,-$\frac{2π}{3}$) | D. | $(4,\frac{2π}{3})$ |
4.已知两个集合A={x|y=ln(-x2+x+2)},$B=\left\{{x\left|{\frac{2e+1}{e-x}≤2}\right.}\right\}$则A∩B=( )
| A. | $[{-\frac{1}{2},2})$ | B. | $({-1,-\frac{1}{2}}]$ | C. | (-1,e) | D. | (2,e) |
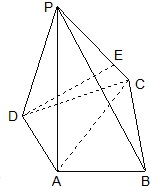 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1,点E在棱PC上,且DE⊥PB.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1,点E在棱PC上,且DE⊥PB.