题目内容
15.已知等差数列{an}满足a2+a4+a2012+a2014=$\frac{32}{π}$${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx,Sn是该数列的前n项的和,则S2015=4030.分析 由定积分的几何意义${∫}_{0}^{1}\sqrt{1-{x}^{2}}dx$=$\frac{1}{4}π×{1}^{2}$.可得a2+a4+a2012+a2014=8.由于数列{an}是等差数列,可得a2+a2014=a4+a2012=a1+a2015,再利用等差数列的前n项和公式即可得出.
解答 解:由定积分的几何意义${∫}_{0}^{1}\sqrt{1-{x}^{2}}dx$=$\frac{1}{4}π×{1}^{2}$=$\frac{1}{4}π$.
∵a2+a4+a2012+a2014=$\frac{32}{π}$${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx=$\frac{32}{π}×\frac{π}{4}$=8,
∵数列{an}是等差数列,
∴a2+a2014=a4+a2012=a1+a2015,
∴2(a2+a2014)=8,
∴a2+a2014=4.
∴S2015=$\frac{2015({a}_{1}+{a}_{2015})}{2}$=4030.
故答案为:4030.
点评 本题考查了微积分基本定理、等差数列的性质及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知tan(π-α)=-2,则$\frac{1}{{cos2α+{{cos}^2}α}}$=( )
| A. | -3 | B. | $\frac{2}{5}$ | C. | 3 | D. | $-\frac{5}{2}$ |
10.已知集合$A=\left\{{\left.x\right|{2^{{x^2}-x-2}}≤1}\right\}$,B={x|y=ln(1-x)},则A∩∁RB=( )
| A. | (1,2) | B. | [1,2] | C. | [-1,1) | D. | (-1,1) |
20.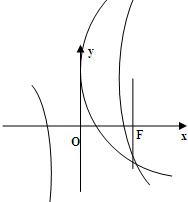 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )| A. | $\sqrt{2}$+1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$-1 |
4.已知两个集合A={x|y=ln(-x2+x+2)},$B=\left\{{x\left|{\frac{2e+1}{e-x}≤2}\right.}\right\}$则A∩B=( )
| A. | $[{-\frac{1}{2},2})$ | B. | $({-1,-\frac{1}{2}}]$ | C. | (-1,e) | D. | (2,e) |