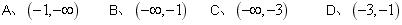题目内容
已知函数f(x)=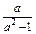 (ax-a-x) (a>0,且a≠1).
(ax-a-x) (a>0,且a≠1).
(1)判断f(x)的单调性;
(2)验证性质f(-x)=-f(x),当x∈(-1,1)时,并应用该性质求满足f(1-m)+f(1-m2)<0的实数m的范围.
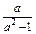 (ax-a-x) (a>0,且a≠1).
(ax-a-x) (a>0,且a≠1).(1)判断f(x)的单调性;
(2)验证性质f(-x)=-f(x),当x∈(-1,1)时,并应用该性质求满足f(1-m)+f(1-m2)<0的实数m的范围.
(1)f(x)在R上为增函数(2)1<m<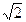
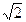
(1)设x1<x2,x1-x2<0,1+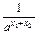 >0.
>0.
若a>1,则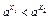 ,
,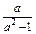 >0,
>0,
所以f(x1)-f(x2)= <0,
<0,
即f(x1)<f(x2),f(x)在(-∞,+∞)上为增函数;
同理,若0<a<1,则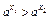 ,
,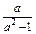 <0,
<0,
f(x1)-f(x2)=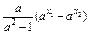 (1+
(1+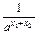 )<0,
)<0,
即f(x1)<f(x2),f(x)在(-∞,+∞)上为增函数.
综上,f(x)在R上为增函数.
(2)f(x)=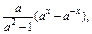 则f(-x)=
则f(-x)=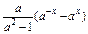 ,
,
显然f(-x)=-f(x).f(1-m)+f(1-m2)<0,
即f(1-m)<-f(1-m2)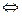 f(1-m)<f(m2-1),
f(1-m)<f(m2-1),
函数为增函数,且x∈(-1,1),故解-1<1-m<m2-1<1,可得1<m<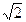 .
.
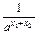 >0.
>0.若a>1,则
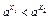 ,
,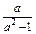 >0,
>0,所以f(x1)-f(x2)=
 <0,
<0,即f(x1)<f(x2),f(x)在(-∞,+∞)上为增函数;
同理,若0<a<1,则
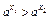 ,
,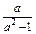 <0,
<0,f(x1)-f(x2)=
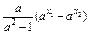 (1+
(1+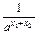 )<0,
)<0,即f(x1)<f(x2),f(x)在(-∞,+∞)上为增函数.
综上,f(x)在R上为增函数.
(2)f(x)=
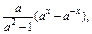 则f(-x)=
则f(-x)=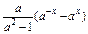 ,
,显然f(-x)=-f(x).f(1-m)+f(1-m2)<0,
即f(1-m)<-f(1-m2)
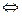 f(1-m)<f(m2-1),
f(1-m)<f(m2-1),函数为增函数,且x∈(-1,1),故解-1<1-m<m2-1<1,可得1<m<
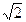 .
.
练习册系列答案
相关题目
 (x≠a).
(x≠a).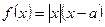
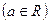 .
.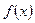 在
在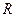 上的奇偶性;
上的奇偶性;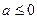 时,求函数
时,求函数 ]上的最大值.
]上的最大值.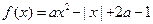
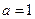 ,求
,求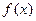 的单调区间;
的单调区间;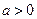 ,设
,设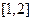 的最小值为
的最小值为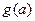 ,求
,求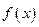 是定义在
是定义在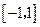 上的奇函数,且
上的奇函数,且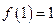 ,若
,若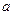 ,
,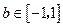 ,
,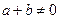 ,有
,有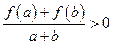 ,判断函数
,判断函数 在
在
 上的最大值为3,最小值为2,求实数
上的最大值为3,最小值为2,求实数 的取值范围.
的取值范围.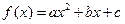 ,其中
,其中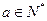 ,
,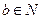 ,
,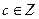 .(1)若
.(1)若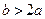 ,且
,且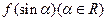 的最大值为2,最小值为
的最大值为2,最小值为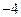 ,求
,求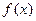 的最小值;(2)若对任意实数
的最小值;(2)若对任意实数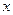 ,不等式
,不等式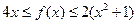 ,且存在
,且存在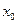 使得
使得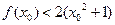 成立,求
成立,求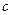 的值.
的值.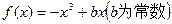 ,且
,且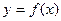 在区间(0,1)上单调递增,并且函数
在区间(0,1)上单调递增,并且函数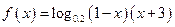 的递减区间是
的递减区间是