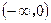题目内容
已知f(x)= (x≠a).
(x≠a).
(1)若a=-2,试证f(x)在(-∞,-2)内单调递增;
(2)若a>0且f(x)在(1,+∞)内单调递减,求a的取值范围.
 (x≠a).
(x≠a).(1)若a=-2,试证f(x)在(-∞,-2)内单调递增;
(2)若a>0且f(x)在(1,+∞)内单调递减,求a的取值范围.
(1)证明见解析(2)0<a≤1
(1)证明 任设x1<x2<-2,则f(x1)-f(x2)=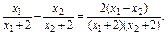
∵(x1+2)(x2+2)>0,x1-x2<0,∴f(x1)<f(x2),∴f(x)在(-∞,-2)内单调递增.
(2)解 任设1<x1<x2,则f(x1)-f(x2)=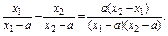
∵a>0,x2-x1>0,∴要使f(x1)-f(x2)>0,只需(x1-a)(x2-a)>0恒成立,
∴a≤1.综上所述知0<a≤1.
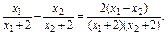
∵(x1+2)(x2+2)>0,x1-x2<0,∴f(x1)<f(x2),∴f(x)在(-∞,-2)内单调递增.
(2)解 任设1<x1<x2,则f(x1)-f(x2)=
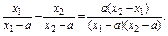
∵a>0,x2-x1>0,∴要使f(x1)-f(x2)>0,只需(x1-a)(x2-a)>0恒成立,
∴a≤1.综上所述知0<a≤1.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 上是增函数,在区间
上是增函数,在区间 上是减函数,则m的值为________。
上是减函数,则m的值为________。
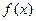 在
在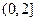 上的单调性,并用定义证明;
上的单调性,并用定义证明;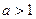 ,求
,求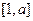 上的最大值
上的最大值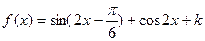
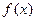 的单调递增区间;
的单调递增区间;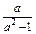 (ax-a-x) (a>0,且a≠1).
(ax-a-x) (a>0,且a≠1).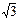 sinx)-1,x∈R
sinx)-1,x∈R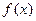 对任意
对任意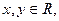 ,都有
,都有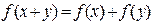 ,且
,且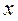 > 0时,
> 0时,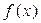 < 0,
< 0,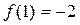 . (1)求
. (1)求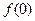 ;
; 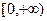 上,求不等式
上,求不等式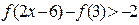 的解集。
的解集。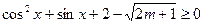 对一切
对一切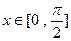 恒成立,则m的取值范围是________________。
恒成立,则m的取值范围是________________。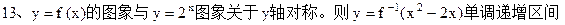 为( )
为( )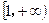 B
B 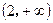 C
C 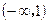 D
D