题目内容
(本题满分15分)已知函数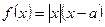
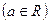 .
.
(I)讨论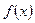 在
在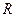 上的奇偶性;
上的奇偶性;
(II)当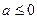 时,求函数
时,求函数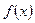 在闭区间[-1,
在闭区间[-1, ]上的最大值.
]上的最大值.
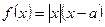
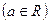 .
.(I)讨论
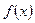 在
在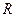 上的奇偶性;
上的奇偶性;(II)当
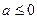 时,求函数
时,求函数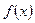 在闭区间[-1,
在闭区间[-1, ]上的最大值.
]上的最大值.(1)f(x)是非奇非偶函数;(2)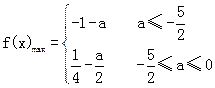
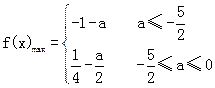
(1)f(x)=|x|(x-a)
当a=0时,f(x)=x·|x|为奇函数
当a≠0时,f(x)=(x-a)|x|,∵f(-a)≠f(a)且f(-a)≠-f(a)
∴f(x)是非奇非偶函数
(2)当a=0时,f(x)=x|x|是奇函数,在R上单调递增
∴当-1≤x≤ 时,f(-1)≤f(x)≤f(
时,f(-1)≤f(x)≤f( )
)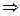 f(x)∈[-1,
f(x)∈[-1,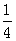 ],此时f(x)max=
],此时f(x)max=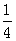
当a<0时,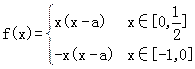
即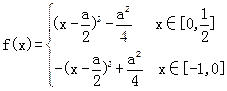
①若-1≤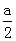 即a≥-2时,f(x)的最大值为f(
即a≥-2时,f(x)的最大值为f(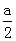 )或f(
)或f( )
)
∵f(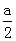 )-f(
)-f( )=
)=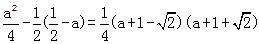
又∵-2≤a<0,则f(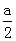 )<f(
)<f( ),∴f(
),∴f( )为最大值
)为最大值
②若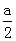 ≤-1即a≤-2,f(x)的最大值为f(-1)或f(
≤-1即a≤-2,f(x)的最大值为f(-1)或f( )
)
∵f(-1)-f( )=(-1-a)-
)=(-1-a)- (
( -a)=-
-a)=-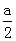 -
-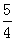
当a≤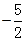 时,f(1)≥f(
时,f(1)≥f( )
)
当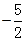 ≤a≤-2时,f(-1)≤f(
≤a≤-2时,f(-1)≤f( )
)
综上可知: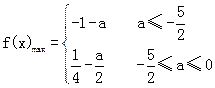
当a=0时,f(x)=x·|x|为奇函数
当a≠0时,f(x)=(x-a)|x|,∵f(-a)≠f(a)且f(-a)≠-f(a)
∴f(x)是非奇非偶函数
(2)当a=0时,f(x)=x|x|是奇函数,在R上单调递增
∴当-1≤x≤
 时,f(-1)≤f(x)≤f(
时,f(-1)≤f(x)≤f( )
)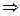 f(x)∈[-1,
f(x)∈[-1,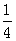 ],此时f(x)max=
],此时f(x)max=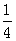
当a<0时,
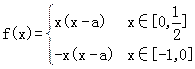
即
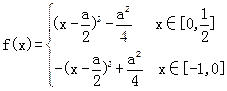
①若-1≤
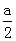 即a≥-2时,f(x)的最大值为f(
即a≥-2时,f(x)的最大值为f(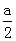 )或f(
)或f( )
)∵f(
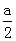 )-f(
)-f( )=
)=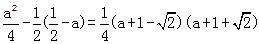
又∵-2≤a<0,则f(
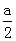 )<f(
)<f( ),∴f(
),∴f( )为最大值
)为最大值②若
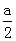 ≤-1即a≤-2,f(x)的最大值为f(-1)或f(
≤-1即a≤-2,f(x)的最大值为f(-1)或f( )
)∵f(-1)-f(
 )=(-1-a)-
)=(-1-a)- (
( -a)=-
-a)=-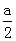 -
-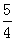
当a≤
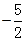 时,f(1)≥f(
时,f(1)≥f( )
)当
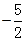 ≤a≤-2时,f(-1)≤f(
≤a≤-2时,f(-1)≤f( )
)综上可知:
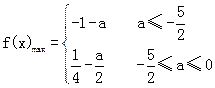

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
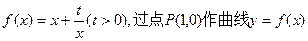 的两条切线PM、PN,切点分
的两条切线PM、PN,切点分 别为M、N.
别为M、N.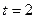 时,求函数
时,求函数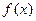 的单调
的单调 递增区间;
递增区间;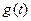 ,试求函数
,试求函数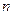 ,在区间
,在区间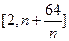 内,总存在m+1个数
内,总存在m+1个数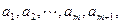 使得不等式
使得不等式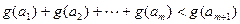 成立,求m的最大值.
成立,求m的最大值.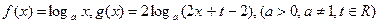
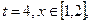 且
且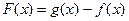 有最小值为2时,求
有最小值为2时,求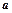 的值;
的值;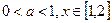 时,有
时,有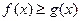 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围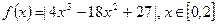 的单调性,并确定它在该区间上的最大值最小值.
的单调性,并确定它在该区间上的最大值最小值.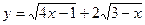 单调递减区间为 。
单调递减区间为 。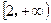 上是增函数,在区间
上是增函数,在区间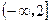 上是减函数,则m的值为________。
上是减函数,则m的值为________。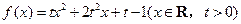 .
.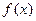 的最小值
的最小值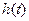 ;
;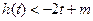 对
对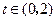 恒成立,求实数
恒成立,求实数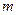 的取值范围.
的取值范围.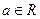 ,函数
,函数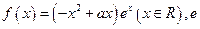 为自然数的底数,
为自然数的底数,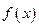 在
在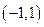 上单调递增,求
上单调递增,求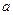 的取值范围;
的取值范围;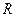 上的单调函数?若是,求出
上的单调函数?若是,求出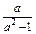 (ax-a-x) (a>0,且a≠1).
(ax-a-x) (a>0,且a≠1).