题目内容
15.给出下列命题:①函数f(x)=sinx,g(x)=sin|x|都是周期函数;
②把函数f(x)=2sin2x图象上每个点的横坐标伸长到原来的4倍,然后再向右平移$\frac{π}{6}$个单位得到的函数解析式可以表示为g(x)=2sin($\frac{1}{2}$x-$\frac{π}{6}$);
③方程sinx=tanx,x∈(-$\frac{π}{2}$,$\frac{π}{2}$)的实数解有3个;
④函数y=cosx,x∈[0,2π]的图象与直线y=1围成的图形面积等于2π;
⑤函数f(x)是偶函数,且图象关于直线x=1对称,则2为f(x)的一个周期.
其中正确的命题是④⑤.(把正确命题的序号都填上).
分析 利用函数的周期性判断①的正误;三角函数的图象变换判断②的正误;函数的零点判断③的正误;利用图形的面积判断④的正误;好的周期性与对称性判断⑤的正误.
解答 解:函数f(x)=sinx是以T=2π为周期的周期函数,g(x)=sin|x|不是周期函数,故①不正确;
把函数f(x)=2sin2x图象上每个点的横坐标伸长到原来的4倍,得到函数f(x)=2sin$\frac{1}{2}$x,然后再向右平移$\frac{π}{6}$个单位得到的函数解析式可以表示为g(x)=2sin($\frac{1}{2}$x-$\frac{π}{12}$);故②错误;
方程sinx=tanx,x∈(-$\frac{π}{2}$,$\frac{π}{2}$)的实数解有1个;故③不正确;
函数y=cosx,x∈[0,2π]的图象与直线y=1围成的图形可以转化为一个底边长2π,高为2的三角形,其面积等于2π,故④正确;
两条相邻的对称轴之间相差半个周期,故当函数f(x)是偶函数,且图象关于直线x=1对称,则2为f(x)的一个周期,故⑤正确;
故答案为:④⑤
点评 本题以命题的真假判断为载体,考查了正弦函数和余弦函数的图象和性质,难度中档.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
6.设集合A={(x,y)||x|+|y|≤1},若动点P(x,y)∈A,则x2+(y-1)2≤2的概率是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | π |
4.(x-2y)7的展开式中的第4项为( )
| A. | -35x4y3 | B. | 280x4y3 | C. | -280x4y3 | D. | 35x4y3 |
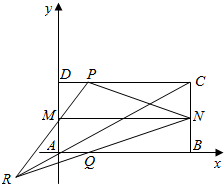 如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),
如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),